Modélisation d'un silencieux réactif simple (Chambre d'expansion)
Contexte Industriel
La problématique du bruit dans les fluides en mouvement
Dans le monde industriel, le bâtiment (CVC - Chauffage, Ventilation, Climatisation) et l'automobile, le transport de fluides (air, gaz d'échappement) est une source majeure de nuisances sonores. Les ventilateurs, compresseurs et moteurs à combustion génèrent des ondes acoustiques de forte énergie qui se propagent efficacement à l'intérieur des conduits, ces derniers agissant comme des guides d'ondes. Sans traitement, ce bruit rayonne à l'extrémité du conduit, causant une pollution sonore inacceptable pour les occupants ou l'environnement.
1. Les deux grandes familles de silencieux
Pour contrer ce phénomène, l'ingénieur acousticien dispose de deux stratégies distinctes, souvent combinées :
A. Les Silencieux Dissipatifs (Absorbants)
Ils utilisent des matériaux poreux ou fibreux (laine de roche, laine de verre, mousses mélamines).
Principe : L'énergie acoustique pénètre dans les pores du matériau. Les frottements visqueux de l'air dans ces micro-cavités transforment l'énergie sonore en chaleur.
Usage : Très efficaces pour les hautes et moyennes fréquences (sifflements, bruit de souffle).
B. Les Silencieux Réactifs (Réfléchissants)
Ils ne contiennent aucun matériau absorbant, seulement du métal (chambres, tubes, chicanes).
Principe : Ils utilisent la géométrie pour créer des ruptures d'impédance. L'onde sonore est forcée de se réfléchir vers la source, empêchant sa transmission vers la sortie.
Usage : Indispensables pour les basses fréquences (ronflements moteur), les environnements sales (graisses, suies) ou très chauds, là où la laine de roche se dégraderait.
2. Le Phénomène Physique : La Rupture d'Impédance
Cet exercice se concentre exclusivement sur le silencieux réactif de type "chambre d'expansion simple". C'est la brique élémentaire des pots d'échappement.
Pour comprendre son fonctionnement, il faut visualiser l'onde sonore non pas comme un simple "bruit", mais comme un flux d'énergie. Dans un tuyau de diamètre constant, l'onde voyage librement. Lorsqu'elle arrive brutalement dans un volume beaucoup plus grand (la chambre), elle rencontre une discontinuité d'Impédance AcoustiqueResistance du milieu à la propagation du son (\(Z = P/U\))..
L'onde ne peut pas s'adapter instantanément à ce changement de "rigidité" du milieu. Par conséquent :
- Une partie de l'onde continue (Transmise).
- Une partie significative rebondit en arrière (Réfléchie).
C'est exactement le même principe que la lumière qui se reflète sur une vitre (changement d'indice de réfraction) ou une vague qui frappe un mur de quai. Le but du jeu pour l'ingénieur est de dimensionner la chambre (\(L\) et \(S\)) pour maximiser cette réflexion aux fréquences gênantes.
Remarque Pédagogique : Pourquoi ce modèle est-il fondamental ?
Cet exercice dépasse le simple cadre de l'acoustique. Il illustre un principe universel de la physique ondulatoire : la réflexion par rupture d'impédance.
- Analogie Électrique : C'est exactement le même phénomène qui se produit dans une ligne de transmission (câble coaxial) lorsque l'impédance de la charge n'est pas adaptée à celle du câble (\(Z_L \neq Z_c\)). Une partie du signal électrique rebondit (ROS - Rapport d'Onde Stationnaire).
- Analogie Optique : C'est comparable à la réflexion de la lumière sur une vitre ou dans une fibre optique. Le changement d'indice de réfraction (l'équivalent optique de l'impédance) entre l'air et le verre force une partie de la lumière à se réfléchir.
- Intérêt Industriel (Le "Pourquoi") : Dans l'industrie automobile ou le bâtiment, les ingénieurs utilisent d'abord ce modèle 1D (Ondes Planes) pour pré-dimensionner les silencieux. C'est rapide, analytique et cela donne les fréquences d'accord principales. Les simulations numériques complexes (3D par Éléments Finis) ne viennent qu'ensuite pour affiner. Comprendre ce modèle simple, c'est comprendre 90% de la physique du problème à basse fréquence.
Objectifs Pédagogiques
À la fin de cet exercice, l'apprenant doit être capable de maîtriser les compétences suivantes :
-
1. Compréhension Physique Fondamentale
Appréhender le mécanisme de réflexion d'onde causé par une rupture d'impédance acoustique. Comprendre qu'un silencieux réactif n'élimine pas l'énergie (contrairement à l'absorption), mais la renvoie vers la source, agissant comme un filtre sélectif géométrique.
-
2. Maîtrise du Calcul Analytique (TL)
Savoir manipuler et appliquer la formule de la Perte par Transmission (Transmission Loss). Identifier l'influence de chaque paramètre : le rapport de surface \(m\) qui pilote l'amplitude maximale de l'atténuation, et la longueur \(L\) qui détermine les fréquences d'accord.
-
3. Analyse Spectrale et Critique
Être capable de prédire les plages de fréquences efficaces (résonances quart d'onde) et les plages critiques d'inefficacité (transparence acoustique aux demi-longueurs d'onde). Savoir critiquer la validité du modèle "Ondes Planes" en fonction de la fréquence de coupure des modes transverses.
Données de l'étude
1. Contexte Industriel et Physique
Les silencieux réactifs sont des composants critiques dans les systèmes de contrôle du bruit, notamment pour les moteurs à combustion interne (pots d'échappement) et les réseaux de ventilation industrielle (CVC). Contrairement aux silencieux dissipatifs (à laine de roche) qui absorbent l'énergie, les silencieux réactifs fonctionnent comme des miroirs acoustiques : ils renvoient l'énergie sonore vers la source.
L'objectif de cet exercice est de dimensionner une "chambre d'expansion simple", qui est la brique élémentaire de tout silencieux complexe. Nous cherchons à déterminer ses performances d'atténuation en fonction de sa géométrie.
2. Description du Système
Le système étudié est constitué d'une conduite rigide cylindrique parcourue par de l'air. Il se décompose en trois zones distinctes :
- Zone 1 (Entrée) : Un conduit d'amenée de diamètre \(d_1\), dans lequel se propage l'onde incidente (le bruit source) et l'onde réfléchie par le silencieux.
- Zone 2 (Chambre) : Une brusque augmentation de section (diamètre \(d_2\)) sur une longueur \(L\). C'est le volume résonant.
- Zone 3 (Sortie) : Un retour au diamètre initial \(d_1\), par lequel s'échappe l'onde transmise (le bruit résiduel). On suppose que ce conduit débouche sur un milieu anéchoïque (pas de retour d'onde venant de l'aval).
3. Hypothèses de Modélisation (Cadre de validité)
Pour appliquer les formules analytiques simples, nous posons les hypothèses suivantes :
- Ondes Planes (1D) : La fréquence étudiée est suffisamment basse pour que la longueur d'onde soit grande devant le diamètre de la chambre (\(f < f_c\)). La pression est uniforme sur toute section droite.
- Conservation du Flux : Aux jonctions \(S_1 \to S_2\) et \(S_2 \to S_1\), il y a continuité de la pression acoustique et du débit volumique.
- Fluide Parfait : On néglige la viscosité de l'air et les pertes thermiques aux parois (pas d'atténuation dissipative).
- Pas d'écoulement moyen : La vitesse de circulation du fluide est négligeable devant la vitesse du son (\(Mach \approx 0\)).
4. Paramètres Numériques
Voici les valeurs spécifiques pour cette étude de cas :
| Paramètre | Symbole | Valeur | Unité | Description / Rôle |
|---|---|---|---|---|
| Diamètre Entrée/Sortie | \(d_1\) | \(0.1\) | \(\text{m}\) | Diamètre des tuyaux de raccordement (standard). |
| Diamètre Chambre | \(d_2\) | \(0.3\) | \(\text{m}\) | Diamètre élargi pour créer la rupture d'impédance. |
| Longueur Chambre | \(L\) | \(0.5\) | \(\text{m}\) | Longueur active déterminant les fréquences d'accord. |
| Célérité du son | \(c\) | \(340\) | \(\text{m/s}\) | Vitesse de propagation dans l'air à \(20^\circ\text{C}\). |
| Masse volumique | \(\rho\) | \(1.2\) | \(\text{kg/m}^3\) | Densité de l'air (utile pour l'impédance \(\rho c\)). |
Schéma Longitudinale (Coupe Axiale)
Vue en Coupe Transversale (A-A)
5. Travail Demandé
Répondez aux questions suivantes pour dimensionner le dispositif :
- Calcul géométrique : Déterminer le taux d'expansion de surface \(m\), paramètre clé de l'efficacité maximale.
- Analyse fréquentielle : Calculer le nombre d'onde \(k\) à la fréquence cible de \(170 \text{ Hz}\).
- Performance : Estimer la Perte par Transmission (TL) à cette fréquence. Le résultat est-il satisfaisant ?
- Points faibles : Identifier les fréquences critiques où le silencieux devient "transparent" (TL = 0).
- Optimisation : À quelle fréquence l'atténuation est-elle théoriquement maximale pour cette longueur \(L\) ?
Les bases théoriques : Physique des Silencieux Réactifs
La modélisation acoustique d'un silencieux repose sur l'étude de la propagation des ondes sonores dans des conduits de sections variables. Contrairement à l'intuition, ce n'est pas le volume de la chambre qui "stocke" le son, mais les réflexions multiples aux interfaces qui empêchent l'énergie de sortir.
1. La Perte par Transmission (Transmission Loss - TL)
Le TL est la grandeur fondamentale pour caractériser l'efficacité d'un filtre acoustique. Il est défini par le rapport logarithmique entre la puissance incidente (\(W_{\text{inc}}\)) qui arrive dans le silencieux et la puissance transmise (\(W_{\text{trans}}\)) qui en ressort.
Définition Énergétique
Pour une chambre d'expansion simple, en supposant une propagation par ondes planes (1D) et sans dissipation (pas de frottement), l'application des équations de continuité (Pression et Débit) aux jonctions permet d'établir la formule analytique suivante :
Formule Analytique du TL (Modèle Ondes Planes)
Analyse des termes de l'équation :
- Le terme "1" : Il représente l'énergie transmise "par défaut". Si les autres termes sont nuls, \(TL = 10 \log(1) = 0 \text{ dB}\) (transparence totale).
- Le terme géométrique \((m - 1/m)^2\) : C'est le "moteur" de l'atténuation. Plus le taux d'expansion \(m = S_2/S_1\) est grand, plus ce terme explose, augmentant le TL. Notez que si \(m=1\) (pas de chambre), le terme s'annule (\(1-1=0\)).
- Le terme spectral \(\sin^2(kL)\) : C'est le "robinet" qui module l'efficacité en fonction de la fréquence. Il oscille entre 0 et 1. Il est responsable des creux et des pics sur la courbe d'atténuation.
2. Le Nombre d'Onde (\(k\)) et la Phase
En mécanique ondulatoire, le nombre d'onde \(k\) joue le rôle d'une "fréquence spatiale". Il indique de combien de radians la phase de l'onde tourne lorsqu'elle parcourt un mètre. C'est le lien direct entre le temps (fréquence \(f\)) et l'espace (longueur \(L\)).
Définition du Nombre d'Onde
Pourquoi est-ce important ici ?
L'efficacité du silencieux dépend du déphasage subi par l'onde lors de son aller-retour dans la chambre. Ce déphasage est donné par le produit \(kL\).
- Si \(kL = \pi\) (ou un multiple), l'onde a fait un tour complet de phase (modulo les réflexions), et peut traverser sans encombre.
- Si \(kL = \pi/2\), l'onde est en quadrature, créant les conditions d'interférence destructive maximale avec l'onde incidente.
3. Mécanisme d'Interférence (Quart d'Onde vs Demi-Onde)
Le silencieux réactif fonctionne comme un filtre en peigne. Son comportement est cyclique en fonction de la fréquence.
A. Transparence (Inefficacité)
Lorsque la longueur de la chambre \(L\) est un multiple de la demi-longueur d'onde (\(L = n \lambda/2\)), l'onde réfléchie revient exactement en phase avec l'onde incidente. Elles s'additionnent pour "forcer" le passage.
Mathématiquement : \(\sin(kL) = 0 \Rightarrow TL = 0 \text{ dB}\).
B. Résonance (Efficacité Maximale)
Lorsque la longueur de la chambre est un multiple impair du quart de longueur d'onde (\(L = (2n+1) \lambda/4\)), l'onde réfléchie revient en opposition de phase (décalage de 180°). Elle tente d'annuler l'onde incidente. L'énergie est alors massivement rejetée vers l'entrée.
Mathématiquement : \(\sin(kL) = 1 \Rightarrow TL \text{ est maximal}\).
Note sur les hypothèses : Toutes ces théories supposent que l'onde reste plane. Si la fréquence est trop élevée (\(f > 0.586 c/d_2\)), l'onde commence à rebondir "en zigzag" sur les parois (modes transverses) et ces formules simples ne s'appliquent plus du tout.
Correction : Modélisation d'un silencieux réactif simple
Question 1 : Calcul du taux d'expansion de surface \(m\)
Principe Physique (La Rupture d'Impédance)
Le fonctionnement du silencieux repose sur la discontinuité brutale de l'impédance acoustique. Lorsqu'une onde sonore voyageant dans un conduit étroit (\(S_1\)) débouche soudainement dans un grand volume (\(S_2\)), elle subit un "choc" géométrique.
L'onde incidente ne peut pas transmettre toute son énergie instantanément à la grande masse d'air de la chambre. Une partie significative de cette énergie "rebondit" contre l'ouverture virtuelle et repart vers la source : c'est l'onde réfléchie. Le paramètre \(m\) quantifie la "violence" de ce changement de section. Plus \(m\) est grand, plus le mur acoustique est "dur".
Mini-Cours : Coefficient de Réflexion
Lien avec la physique fondamentale :
Le taux d'expansion \(m = S_2/S_1\) détermine directement le coefficient de réflexion en pression \(R\) à l'interface d'entrée (en basse fréquence) :
Si \(m=1\) (pas de changement), \(R=0\) (tout passe). Si \(m \to \infty\) (mur rigide), \(R \to 1\) (réflexion totale). Dans notre exercice, un grand \(m\) est donc souhaitable pour maximiser \(R\) et donc le TL.
Remarque Pédagogique (Piège Classique)
⚠️ Confusion Diamètre vs Surface
L'erreur la plus fréquente chez les étudiants est de calculer le rapport des diamètres (\(d_2/d_1\)) et de l'appeler \(m\). C'est faux ! L'acoustique est une histoire de flux de volume, donc de SURFACES.
Rappelez-vous : Si vous doublez le diamètre d'un tuyau, vous quadruplez sa surface de passage (\(2^2 = 4\)). L'effet acoustique est donc bien plus fort que ce que l'intuition visuelle suggère.
Normes et Standards
Dans l'industrie (ISO 11820 pour les mesures de silencieux in-situ), le rapport de section est le premier paramètre vérifié lors du pré-dimensionnement. Pour les applications CVC, on vise souvent \(m > 4\) pour avoir une atténuation perceptible.
Formule(s) Analytiques
Définition mathématique
Surface d'une section circulaire
Taux d'expansion (m)
En injectant la formule de la surface, les constantes \(\pi/4\) se simplifient :
Hypothèses de Calcul
Pour que ce calcul géométrique simple soit valide acoustiquement, nous supposons :
- Parois indéformables : Le métal ne vibre pas (pas de perte par transmission pariétale).
- Changement brusque : L'élargissement est une "marche" à 90°, pas un cône progressif (qui réduirait la réflexion).
- Centrage : Les axes des deux cylindres sont confondus (symétrie axiale), évitant la création de modes asymétriques complexes.
Donnée(s) Numériques
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Diamètre conduit (Entrée) | \(d_1\) | 0.1 | \(\text{m}\) (100 mm) |
| Diamètre chambre (Corps) | \(d_2\) | 0.3 | \(\text{m}\) (300 mm) |
Astuces de Calcul Mental
Inutile de calculer les surfaces \(S_1\) et \(S_2\) séparément (ce qui introduirait des erreurs d'arrondi avec \(\pi\)). Calculez simplement le rapport des diamètres (ici \(0.3/0.1 = 3\)) et élevez-le au carré de tête (\(3^2 = 9\)). C'est plus rapide et plus précis.
Schémas Situation Initiale (Comparaison des Sections)
Vue de Face : Section S1 (Entrée)
Vue de Face : Section S2 (Chambre)
Détail des Calculs
Étape 1 : Calcul du ratio linéaire (adimensionnel)
Nous commençons par comparer les dimensions linéaires. C'est l'étape la plus simple mais elle donne l'ordre de grandeur. Nous divisons le diamètre de la chambre par celui du tuyau d'entrée.
Le facteur d'échelle linéaire est de 3. La chambre est trois fois plus large que le tuyau.
Étape 2 : Passage aux surfaces (Loi quadratique)
L'acoustique est régie par les flux d'énergie qui traversent une section. Or, l'aire d'un cercle est proportionnelle au carré de son rayon (ou diamètre). Pour obtenir le rapport des surfaces \(m\), nous devons élever le rapport linéaire au carré.
Résultat : Le taux d'expansion est de 9. Cela signifie que l'onde sonore, confinée dans une section \(S\), se dilue subitement dans une section \(9S\).
Schémas de Synthèse (Visualisation du Résultat)
Représentation Proportionnelle
L'expansion brutale de S1 vers S2 (x9) est le moteur de l'atténuation.
Réflexions et Analyse
La valeur \(m=9\) est élevée. Dans la pratique, un taux d'expansion supérieur à 4 est considéré comme efficace pour un silencieux réactif. Avec \(m=9\), nous pouvons nous attendre à une très bonne performance acoustique (atténuation forte), au prix d'un encombrement important (diamètre 30cm pour un tuyau de 10cm).
FAQ Anticipée
Est-ce que \(m\) peut être inférieur à 1 ?
Oui, si la "chambre" est plus petite que le tuyau (rétrécissement). Cela créerait aussi une rupture d'impédance et des réflexions, mais générerait énormément de pertes de charge aérauliques (résistance à l'écoulement de l'air), ce qui est mauvais pour le ventilateur ou le moteur.
A vous de jouer
Si le diamètre de la chambre était doublé (\(d_2 = 0.6 \text{ m}\)), que vaudrait \(m\) ? (Indice : le rapport des diamètres devient 6).
📝 Mémo Rapide
\(m = (\text{Grand Diamètre} / \text{Petit Diamètre})^2\). C'est le carré qui fait la puissance du silencieux.
Question 2 : Calcul du nombre d'onde \(k\)
Principe Physique (La "Fréquence Spatiale")
Pour comprendre le nombre d'onde \(k\), il faut faire une analogie avec le temps. En physique, la fréquence \(f\) (ou la pulsation \(\omega\)) nous dit à quelle vitesse l'onde oscille "sur place" au fil du temps. Le nombre d'onde \(k\), lui, nous dit à quelle vitesse l'onde oscille "dans l'espace" lorsqu'on se déplace le long du tuyau.
C'est une densité de phase : il indique combien de radians de phase sont accumulés par l'onde à chaque mètre parcouru. Plus \(k\) est grand, plus les "vagues" de pression sont serrées les unes contre les autres (longueur d'onde courte).
Mini-Cours : L'équation d'onde
Lien mathématique fondamental :
Une onde plane progressive harmonique de pression \(p(x,t)\) s'écrit généralement :
Dans cette équation :
- \(\omega t\) est la phase temporelle (\(\text{rad/s} \times \text{s} = \text{rad}\)).
- \(kx\) est la phase spatiale (\(\text{rad/m} \times \text{m} = \text{rad}\)).
Pour que l'équation soit dimensionnellement correcte, \(k\) doit forcément être en radians par mètre. Il est relié à la longueur d'onde \(\lambda\) (la distance spatiale d'un cycle complet \(2\pi\)) par la relation : \(k = \frac{2\pi}{\lambda}\).
Remarque Pédagogique (Unités et Pièges)
Attention aux confusions !
Ne confondez pas :
- Fréquence \(f\) [Hz] : Cycles par seconde.
- Pulsation \(\omega\) [rad/s] : Radians par seconde (\(\omega = 2\pi f\)).
- Nombre d'onde \(k\) [rad/m] : Radians par mètre (\(k = \omega / c\)).
En spectroscopie (chimie), on utilise parfois \(\tilde{\nu} = 1/\lambda\) (en \(\text{cm}^{-1}\)) qu'on appelle aussi "nombre d'onde". En acoustique, on inclut toujours le facteur \(2\pi\).
Normes
ISO 80000-3 (Grandeurs et unités d'espace et de temps) définit officiellement le nombre d'onde angulaire (angular wavenumber) comme le quotient de \(2\pi\) par la longueur d'onde.
Formule(s) Analytiques
Définitions croisées
Relation de dispersion (milieu non dispersif)
Lien avec la longueur d'onde
Hypothèses de Calcul
Pour que \(k\) soit une constante simple, nous supposons :
- Milieu homogène : La température est constante partout (donc \(c\) est constant). Si la chambre était chaude (échappement), \(k\) changerait.
- Milieu au repos : Pas de vent. Si l'air bougeait à une vitesse \(V\), on aurait deux nombres d'onde différents : \(k^+\) (vers l'aval) et \(k^-\) (vers l'amont), modifiés par le nombre de Mach.
Donnée(s) Numériques
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Fréquence cible | \(f\) | 170 | \(\text{Hz}\) (cycles/s) |
| Célérité du son | \(c\) | 340 | \(\text{m/s}\) |
Astuces de Calcul Mental
Avant de sortir la calculatrice, regardez les chiffres ! \(170\) est exactement la moitié de \(340\). Donc le ratio \(f/c\) vaut \(0.5\). Multiplié par \(2\pi\), le résultat est immédiat : \(\pi\). Les sujets d'examens sont souvent conçus avec ces "chiffres ronds" acoustiques.
Schémas Situation Initiale (Visualisation Spatiale)
Longueur d'onde \(\lambda\)
Détail des Calculs
Étape 1 : Calcul de la pulsation angulaire \(\omega\)
Nous convertissons d'abord la fréquence (tours par seconde) en radians par seconde. C'est la "vitesse de rotation" du phaseur.
Étape 2 : Lien temporel -> spatial (Division par c)
L'onde parcourt \(c\) mètres chaque seconde. Pour savoir de combien la phase tourne par mètre, nous divisons la vitesse de rotation temporelle par la vitesse de déplacement.
Étape 3 : Simplification et Résultat Exact
Plutôt que de traîner des décimales infinies, nous simplifions la fraction. On remarque que \(340 = 2 \times 170\).
Résultat : \(k = \pi\) radians par mètre. Cela signifie que sur une distance de 1 mètre, la phase de l'onde tourne exactement de \(\pi\) radians (soit un demi-tour, ou 180°).
Schémas Validation (Interprétation du Résultat)
Sens physique de k = π
Réflexions et Analyse
Avoir \(k = \pi\) est un résultat très "propre". Cela implique que la longueur d'onde est \(\lambda = 2\pi/k = 2\) mètres. Comme notre chambre fait \(L=0.5\) m, le rapport \(L/\lambda\) sera de \(0.5/2 = 1/4\). Nous anticipons donc un phénomène de quart d'onde, crucial pour la suite.
Points de vigilance
Erreur de calculatrice (Radian vs Degré)
Si vous utilisez votre calculatrice pour calculer le sinus plus tard, assurez-vous qu'elle est en mode RADIAN. Ici \(kL = \pi/2\). Si vous êtes en mode DEGRÉ, \(\sin(\approx 1.57)\) donnera un résultat proche de 0 (faux), alors que \(\sin(\pi/2 \text{ rad})\) donne 1 (vrai).
Points à Retenir
- \(k\) augmente linéairement avec la fréquence (\(k \propto f\)).
- Les sons graves (basse fréq.) ont un petit \(k\) (phase change lentement dans l'espace).
- Les sons aigus (haute fréq.) ont un grand \(k\) (phase change très vite).
Le saviez-vous ?
En spectroscopie infrarouge, les chimistes utilisent aussi le "nombre d'onde", mais défini comme \(\sigma = 1/\lambda\) (l'inverse de la longueur d'onde), souvent exprimé en \(\text{cm}^{-1}\). En physique acoustique, on garde le facteur \(2\pi\) pour simplifier les dérivées harmoniques.
FAQ
Est-ce que \(k\) dépend du diamètre du tuyau ?
Non, tant qu'on reste en ondes planes. \(k\) ne dépend que de la fréquence et du milieu (vitesse du son). Le diamètre intervient pour définir la fréquence limite où l'onde cesse d'être plane.
A vous de jouer
Calculer \(k\) pour la fréquence double \(f = 340 \text{ Hz}\).
📝 Mémo
\(k\) : combien de radians je tourne par mètre parcouru.
Question 3 : Perte par Transmission (TL) à \(170 \text{ Hz}\)
Principe Physique (L'Évaluation de Performance)
Maintenant que nous avons caractérisé la géométrie (\(m=9\)) et la propagation (\(k=\pi\)), nous allons calculer l'efficacité réelle du silencieux à la fréquence cible. Le Transmission Loss (TL) est notre "juge de paix". Il nous dit, sur une échelle logarithmique, quelle quantité d'énergie est stoppée.
À \(170 \text{ Hz}\), nous allons vérifier si la chambre joue son rôle de "bouchon acoustique" ou si elle laisse passer le son.
Mini-Cours : Comprendre les Décibels (dB)
Lecture du résultat :
Le TL n'est pas une simple soustraction de pression, c'est un ratio de puissance.
- \(TL = 0 \text{ dB}\) : \(100\%\) de l'énergie passe (Inefficace).
- \(TL = 3 \text{ dB}\) : \(50\%\) de l'énergie est bloquée.
- \(TL = 10 \text{ dB}\) : \(90\%\) de l'énergie est bloquée (Divisé par 10).
- \(TL = 20 \text{ dB}\) : \(99\%\) de l'énergie est bloquée (Divisé par 100).
Remarque Pédagogique
Nous avons choisi \(170 \text{ Hz}\) spécifiquement parce que cela correspond à une condition de résonance particulière (voir calculs). Dans un vrai projet, on calculerait le TL sur tout le spectre (ex: de 50 à 1000 Hz) pour voir la courbe complète.
Normes
ISO 11820 : Norme acoustique pour la mesure in situ des silencieux. Elle définit précisément les conditions de mesure du TL (salle anéchoïque ou tube à impédance).
Formule(s) Analytiques
L'équation maîtresse
Cette formule sépare clairement deux contributions :
1. Le terme géométrique \((m - 1/m)^2\) : Le potentiel maximum.
2. Le terme spectral \(\sin^2(kL)\) : Le taux d'activation de ce potentiel (entre 0 et 1).
Hypothèses
Le calcul suppose que le tuyau de sortie est "adapté" (anéchoïque), c'est-à-dire que le son qui sort ne revient jamais. Si le tuyau de sortie débouchait sur un mur, il y aurait des réflexions supplémentaires non prises en compte ici.
Donnée(s) Numériques (Rappel)
| Paramètre | Valeur | Source |
|---|---|---|
| Taux d'expansion \(m\) | 9 | Question 1 |
| Nombre d'onde \(k\) | \(\pi \text{ rad/m}\) | Question 2 |
| Longueur \(L\) | \(0.5 \text{ m}\) | Énoncé |
Astuces de Calcul
Toujours calculer le terme \(\sin(kL)\) en premier. S'il vaut 0, tout s'annule et \(TL=0\). S'il vaut 1, on est au max. C'est le "check" rapide avant de se lancer dans les logarithmes.
Schémas Situation Initiale
Configuration à 170 Hz
Détail des Calculs
Étape 1 : Analyse du terme spectral (Phase)
On calcule l'argument du sinus, qui représente le déphasage acoustique sur la longueur de la chambre :
C'est une valeur remarquable ! \(\frac{\pi}{2}\) correspond à un quart de tour de cercle trigonométrique (90°). La fonction sinus y est maximale :
Conclusion intermédiaire : À 170 Hz, le silencieux fonctionne à 100% de son potentiel géométrique.
Étape 2 : Analyse du terme géométrique (Amplitude)
On calcule le facteur de puissance lié au changement de section \(m=9\). D'abord le terme entre parenthèses :
On élève ce résultat au carré (car l'énergie est proportionnelle au carré de la pression/vitesse) :
Étape 3 : Calcul final du TL
On assemble les morceaux dans le logarithme.
Ce nombre (environ 21) est le rapport de réduction de puissance. La puissance incidente est 21 fois supérieure à la puissance transmise. Il ne reste plus qu'à convertir en décibels :
Schémas Validation
Résultat
Réflexions et Interprétation
Le résultat de \(13.2 \text{ dB}\) est le maximum absolu que l'on peut obtenir avec un rapport de surface \(m=9\). Aucune autre fréquence ne donnera une meilleure atténuation pour cette géométrie. Si l'on veut plus d'atténuation (ex: 20 dB), il faudrait augmenter \(m\) (élargir la chambre) ou mettre plusieurs chambres en série.
Points de vigilance
Logarithme Base 10 vs Népérien
Sur votre calculatrice, utilisez la touche log (base 10) et non ln (base e).
\(10 \ln(20.7) \approx 30 \text{ dB}\), ce qui est faux et surestime grandement la performance !
Points à Retenir
La condition \(kL = \pi/2\) correspond à \(L = \lambda/4\). C'est le principe du résonateur quart d'onde : l'onde réfléchie parcourt \(2 \times L = \lambda/2\), revenant en opposition de phase pour annuler l'onde incidente.
Le saviez-vous ?
Une atténuation de \(13 \text{ dB}\) peut sembler modeste, mais acoustiquement, cela transforme un bruit "insupportable" en un bruit "supportable". C'est l'équivalent de s'éloigner de la source d'un facteur 4 ou 5.
FAQ
Peut-on obtenir 50 dB avec une seule chambre ?
Théoriquement oui, si \(m\) est gigantesque. Mais en pratique, non : les dimensions deviendraient absurdes et les modes transverses ruineraient l'efficacité bien avant.
A vous de jouer
Si \(m=1\) (tube droit sans chambre), que vaut le TL ? (Vérifiez que la formule donne bien 0).
📝 Mémo
Max efficacité à \(\lambda/4\). C'est le "sweet spot" du design.
Question 4 : Fréquences de passage (\(TL = 0\))
Principe Physique (La Transparence Acoustique)
Un silencieux réactif ne bloque pas le son de manière uniforme. Il se comporte comme un filtre en peigne. Il existe des fréquences spécifiques où le dispositif devient acoustiquement "invisible" ou transparent.
À ces fréquences, les ondes réfléchies par l'interface de sortie (fin de la chambre) reviennent vers l'entrée avec un déphasage tel qu'elles s'annulent ou compensent parfaitement les réflexions de l'entrée. Résultat : l'énergie traverse la chambre sans aucune atténuation, comme si le tuyau était droit et continu. C'est le pire scénario pour l'acousticien.
Mini-Cours : L'Adaptation d'Impédance par Demi-Onde
Analogie avec les lignes de transmission :
En physique ondulatoire, un tronçon de ligne (ici la chambre) de longueur \(L = \lambda/2\) (demi-longueur d'onde) possède une propriété remarquable : il reporte l'impédance de sortie directement à l'entrée, sans modification.
Comme le tuyau de sortie a le même diamètre (\(d_1\)) que le tuyau d'entrée, son impédance est identique (\(Z_1\)). Lorsque \(L = \lambda/2\), la chambre "connecte" virtuellement l'entrée à la sortie. L'onde incidente "voit" une impédance \(Z_1\) au lieu de l'impédance de la chambre. Il n'y a donc aucune rupture d'impédance apparente, donc aucune réflexion, et donc un \(TL = 0 \text{ dB}\).
Remarque Pédagogique
Le talon d'Achille du réactif
C'est la différence fondamentale avec les silencieux dissipatifs (laine de verre) dont l'efficacité augmente généralement avec la fréquence. Le silencieux réactif "s'effondre" périodiquement. Si le bruit de votre moteur se situe pile sur une de ces fréquences (ex: 340 Hz), le silencieux sera totalement inutile !
Normes
Les normes de test (ISO 7235) exigent des balayages en fréquence précis pour identifier ces "trous" de performance, qui ne doivent pas coïncider avec les fréquences d'excitation de la machine (fréquence de rotation des pales, etc.).
Formule(s) Mathématique
Condition d'annulation
Le TL est nul lorsque le terme logarithmique vaut 0, c'est-à-dire quand l'argument du log vaut 1. Cela implique que le terme en sinus doit s'annuler :
Hypothèses
On suppose que le comportement reste linéaire et que la longueur \(L\) est la longueur géométrique exacte (sans correction de longueur due aux effets de bout, qui serait nécessaire pour une très haute précision).
Donnée(s) Numériques
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Longueur de chambre | \(L\) | \(0.5\) | \(\text{m}\) |
| Vitesse du son | \(c\) | \(340\) | \(\text{m/s}\) |
Astuces
Rappelez-vous : Le sinus s'annule tous les \(\pi\) (0, \(\pi\), \(2\pi\), ...). C'est votre base pour trouver les multiples \(n\).
Schémas Situation Initiale
Détail des Calculs
Étape 1 : Traduire la condition mathématique \(\sin(x)=0\)
La fonction sinus s'annule lorsque son angle est un multiple entier de \(\pi\). Nous posons donc l'équation fondamentale :
où \(n\) est un nombre entier positif (\(1, 2, 3, \dots\)). \(n=0\) correspondrait à une fréquence nulle (statique), ce qui n'a pas de sens en acoustique.
Étape 2 : Expliciter le nombre d'onde \(k\)
Nous savons que \(k\) dépend de la fréquence \(f\). On remplace \(k\) par \(2\pi f / c\) :
Notre inconnue est la fréquence \(f\).
Étape 3 : Isolation de la fréquence \(f\)
On simplifie l'équation. Les \(\pi\) sont présents des deux côtés et s'annulent :
Cette formule \(f = n \frac{c}{2L}\) est très célèbre : c'est la série harmonique d'un tuyau ouvert-ouvert (ou corde vibrante). Les fréquences de passage sont simplement les multiples de la fréquence fondamentale \(c/2L\).
Étape 4 : Application Numérique
On injecte nos valeurs \(c=340\) et \(L=0.5\) :
On calcule les premiers modes :
Pour \(n=1\) : \(f_1 = 340 \text{ Hz}\).
Pour \(n=2\) : \(f_2 = 680 \text{ Hz}\).
Pour \(n=3\) : \(f_3 = 1020 \text{ Hz}\).
Schémas Validation (L'Onde Entière)
Mode n=1 : Demi-Onde (\(L = \lambda/2\))
La longueur de la chambre contient exactement une demi-onde. L'entrée et la sortie sont dans le même état vibratoire.
Réflexions et Analyse
Nous avons trouvé que la première fréquence critique est de \(340 \text{ Hz}\). À cette fréquence, la longueur d'onde est de \(1 \text{ m}\). La chambre de \(0.5 \text{ m}\) correspond donc bien à \(\lambda / 2\). C'est cohérent. Si le moteur tourne à un régime générant une fréquence fondamentale de \(340 \text{ Hz}\) (ou ses harmoniques), le silencieux sera inopérant.
Points de vigilance
Ne confondez pas ces fréquences (\(TL=0\)) avec les fréquences de résonance transversale (haute fréquence). Ici, nous sommes toujours dans le domaine plan, mais dans une configuration de résonance longitudinale de transmission.
Points à Retenir
Règle d'Or :
Pas d'atténuation si \(L\) est un multiple de \(\frac{\lambda}{2}\).
\(L = 1 \times \frac{\lambda}{2}, \quad 2 \times \frac{\lambda}{2}, \quad \dots\)
Le saviez-vous ?
Pour combler ces "trous" dans le spectre d'atténuation, les concepteurs placent souvent deux chambres de longueurs différentes en série (\(L_1 \neq L_2\)). Les trous de l'une sont comblés par les pics de l'autre !
FAQ
Est-ce qu'ajouter de la laine de roche aide ?
Oui ! Transformer le silencieux réactif en silencieux hybride permet d'absorber l'énergie justement à ces fréquences de passage, lissant ainsi la courbe de performance.
A vous de jouer
Quelle est la 2ème fréquence de passage ?
📝 Mémo
Évitez les longueurs multiples de la demi-onde pour les fréquences à traiter.
Question 5 : Fréquence d'atténuation maximale
Principe Physique (La "Magie" du Quart d'Onde)
Nous cherchons maintenant les fréquences où le silencieux est le plus performant (pics du graphique TL). Cela se produit lorsque l'onde qui revient de la fin de la chambre (\(x=L\)) arrive à l'entrée (\(x=0\)) exactement en opposition de phase avec l'onde qui tente d'entrer.
Pour que deux signaux s'annulent, ils doivent être décalés d'une demi-longueur d'onde (\(\lambda/2\)). Or, l'onde dans la chambre fait un aller-retour (distance \(2L\)). Si cette distance \(2L\) vaut \(\lambda/2\), alors l'annulation est maximale. Cela implique \(L = \lambda/4\). C'est le principe du "Quart d'Onde".
Mini-Cours : Le Transformateur d'Impédance Acoustique
Analogie Électrique :
Une ligne de transmission de longueur \(\lambda/4\) a la propriété d'inverser les impédances. Si la sortie de la chambre est vue comme une impédance faible (ou forte), vue de l'entrée à travers un quart d'onde, elle paraîtra forte (ou faible).
En acoustique, la chambre de longueur \(L=\lambda/4\) transforme l'impédance de sortie \(Z_{\text{sortie}}\) en une impédance d'entrée \(Z_{\text{entrée}} \approx Z_{\text{chambre}}^2 / Z_{\text{sortie}}\). Cette transformation crée une désadaptation maximale à l'entrée du silencieux, maximisant la réflexion de l'énergie vers la source.
Remarque Pédagogique
Attention à la série harmonique !
Contrairement aux cordes de guitare ou aux tubes ouverts qui résonnent à \(f, 2f, 3f\dots\) (tous les entiers), l'efficacité maximale du silencieux réactif se produit pour les harmoniques impairs uniquement : \(1f, 3f, 5f\dots\).
Normes
Dans le dimensionnement des lignes d'échappement, on cale souvent ce "pic" sur la fréquence d'allumage du moteur au régime de croisière (ex: 3000 tr/min).
Formule(s) Analytiques
Condition de Maximisation
Le terme \(\sin^2(kL)\) dans la formule du TL atteint son maximum (1) lorsque l'angle vaut \(90^\circ\) (\(\pi/2\) radians) ou un multiple impair :
Pour la première fréquence (la plus basse, fondamentale), on prend \(n=0\), donc \(kL = \pi/2\).
Hypothèses
On suppose que la longueur "acoustique" est égale à la longueur géométrique \(L\). En réalité, l'air qui oscille aux extrémités "déborde" un peu (correction de longueur), mais nous négligeons cet effet ici.
Donnée(s) Numériques
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Longueur active | \(L\) | \(0.5\) | \(\text{m}\) |
| Célérité | \(c\) | \(340\) | \(\text{m/s}\) |
Astuces
Pour trouver la fréquence max rapidement : C'est la moitié de la première fréquence de transparence (calculée à la Q4). Si le trou est à 340 Hz, le pic est à 170 Hz.
Schémas Situation Initiale
Objectif : Tenir un quart d'onde
Détail des Calculs
Étape 1 : Poser la condition de résonance (sinus max)
Nous cherchons la fréquence la plus basse (\(n=0\)) pour laquelle le terme sinus vaut 1. L'argument du sinus doit être \(\pi/2\) :
Étape 2 : Remplacer k par la fréquence
On utilise la relation de dispersion \(k = \frac{2\pi f}{c}\) :
Nous avons une équation avec une seule inconnue : \(f\).
Étape 3 : Isoler f (Formule du quart d'onde)
On simplifie par \(\pi\) des deux côtés. Puis on déplace les termes pour isoler \(f\) :
C'est la formule canonique du premier mode propre d'un tube fermé-ouvert (ou quart d'onde).
Étape 4 : Application Numérique
On remplace par les valeurs : \(c = 340 \text{ m/s}\) et \(L = 0.5 \text{ m}\).
Le silencieux est donc "accordé" sur \(170 \text{ Hz}\). C'est à cette fréquence qu'il offrira ses meilleurs 13.2 dB d'atténuation.
Schémas Validation (L'Onde Stationnaire)
Mode n=0 : Quart d'Onde (\(L = \lambda/4\))
L'onde parcourt un quart de cycle, est réfléchie, et parcourt un autre quart. Total : demi-cycle (\(\pi\)). Opposition de phase parfaite.
Réflexions et Analyse
\(170 \text{ Hz}\) est une fréquence relativement basse (bas-médium). C'est typique des bruits d'échappement ou de ventilation. Pour traiter des fréquences encore plus basses (ex: 50 Hz), il faudrait augmenter \(L\) proportionnellement. \(L_{50\text{Hz}} = 340 / (4 \times 50) = 1.7 \text{ m}\). Les silencieux basse fréquence sont donc nécessairement volumineux.
Points de vigilance
Harmoniques Impairs Seulement !
Attention, la prochaine fréquence d'efficacité maximale n'est pas \(2 \times 170\) (340 Hz, qui est un trou !), mais \(3 \times 170 = 510 \text{ Hz}\). Puis \(5 \times 170 = 850 \text{ Hz}\). La série est : \(f_0, 3f_0, 5f_0, 7f_0 \dots\)
Points à Retenir
Formule Clé :
Fréquence optimale : \(f_{\text{opt}} = \frac{c}{4L}\).
À cette fréquence, l'atténuation dépend uniquement de \(m\).
Le saviez-vous ?
Cette logique de "quart d'onde" est aussi utilisée pour les traitements anti-reflets sur les lunettes (couches minces optiques d'épaisseur \(\lambda/4\)) ! La physique est universelle.
FAQ
Que se passe-t-il si je change le diamètre \(d_2\) ?
Cela change l'amplitude du pic (plus de dB), mais cela ne change pas la fréquence du pic (toujours 170 Hz), car la fréquence ne dépend que de \(L\).
A vous de jouer
Quelle est la prochaine fréquence max (\(n=1\)) ? Rappel : facteur 3.
📝 Mémo
Le quart d'onde (\(L=\lambda/4\)) verrouille l'entrée.
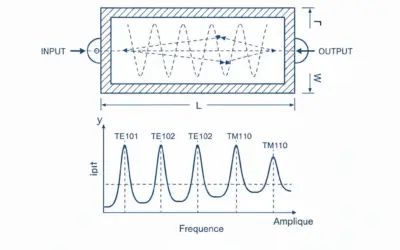
Schéma Bilan de l'Exercice
Ce schéma résume l'ensemble des grandeurs calculées et l'état vibratoire du système à la fréquence critique de 170 Hz.
1. Analyse Physique du Phénomène
Le schéma ci-dessus illustre ce qui se passe à l'intérieur de la chambre d'expansion à la fréquence précise de \(170 \text{ Hz}\). C'est un cas de résonance quart d'onde.
- La géométrie : La longueur de la chambre \(L = 0.5 \text{ m}\) correspond exactement à un quart de la longueur d'onde du son (\(\lambda = 2 \text{ m}\)).
- L'interférence : L'onde incidente pénètre dans la chambre et se réfléchit contre la paroi de sortie (changement de section). L'onde réfléchie parcourt le chemin inverse. À cette fréquence spécifique, les ondes incidentes et réfléchies se superposent de manière à créer une onde stationnaire.
- Le Ventre de Pression : La courbe rouge montre l'enveloppe de la pression acoustique. On observe un maximum d'amplitude (appelé "Ventre") au centre de la zone, et des minima (appelés "Noeuds") aux connexions. Cette distribution d'énergie empêche la propagation efficace vers la sortie.
2. Mécanisme d'Atténuation (Pourquoi ça marche ?)
La Désadaptation d'Impédance
Le silencieux réactif ne "tue" pas l'énergie sonore en la transformant en chaleur (comme le ferait de la laine de verre). Il fonctionne comme un miroir. La brusque variation de surface (passage de \(d_1\) à \(d_2\)) crée une rupture d'impédance acoustique.
L'onde sonore "voit" un élargissement brutal et ne peut pas s'adapter instantanément. Une grande partie de son énergie rebondit alors vers la source. C'est ce retour d'énergie qui diminue le niveau sonore transmis en sortie.
3. Bilan Énergétique (Interprétation du TL)
Nous avons calculé une Perte par Transmission (TL) de \(13.2 \text{ dB}\). Mais concrètement, qu'est-ce que cela signifie en termes de puissance ?
Le lien entre les décibels et le rapport de puissance est logarithmique. Si \(P_{\text{inc}}\) est la puissance incidente et \(P_{\text{trans}}\) la puissance transmise :
Conclusion Chiffrée :
Seulement 4.8% de l'énergie sonore incidente traverse le silencieux.
Plus de 95% de l'énergie est réfléchie vers l'entrée ! C'est un résultat très efficace pour un dispositif purement géométrique sans matériau absorbant.
4. Limites du Modèle
Ce bilan est idéal. Dans la réalité, plusieurs facteurs peuvent modifier ces résultats :
- Écoulement du fluide : Si de l'air circule vite (vitesse \(V > 0\)), cela modifie le nombre d'onde \(k\) (effet Doppler convectif) et peut générer du "bruit propre" (turbulences).
- Température : Si la température change (ex: pot d'échappement), la célérité \(c\) change, et donc les fréquences d'accord (\(170 \text{ Hz}\)) se décalent.
- Modes transverses : Si le diamètre \(d_2\) devient trop grand par rapport à la longueur d'onde, l'hypothèse d'ondes planes ne tient plus (apparition de modes radiaux complexes).
📝 Grand Mémo : Ce qu'il faut retenir absolument
Voici la synthèse approfondie des concepts physiques et des règles de dimensionnement pour les silencieux réactifs :
-
🔑
Point Clé 1 : Le Rôle de la Géométrie (L'Amplitude)
Le niveau d'atténuation maximal (la "hauteur" des pics sur le graphique) dépend exclusivement du rapport de surfaces, noté \(m\).
- Le principe physique : Plus le diamètre de la chambre \(d_2\) est grand par rapport au conduit \(d_1\), plus la rupture d'impédance est violente. L'onde sonore incidente perçoit l'élargissement brusque comme un "mur mou" et rebondit vers la source.
-
Formule simplifiée : Pour des grands rapports d'expansion (\(m > 4\)), le \(TL_{\text{max}}\) peut être approximé par :
\(TL_{\text{max}} \approx 20 \log_{10}(m) - 6 \text{ dB}\).
Exemple : Si vous doublez le diamètre de la chambre, \(m\) est multiplié par 4, et vous gagnez environ 12 dB d'atténuation maximale.
-
📐
Point Clé 2 : Le Rôle de la Longueur (Le Filtrage)
La longueur de la chambre \(L\) ne change pas la performance maximale, mais elle détermine QUELLES fréquences seront atténuées. Le silencieux agit comme un filtre sélectif (filtre en peigne).
-
Condition d'Efficacité Maximale (Résonance Quart d'Onde) :
L'atténuation est maximale lorsque la longueur de la chambre correspond à un nombre impair de quarts de longueur d'onde : \(L = (2n+1) \frac{\lambda}{4}\). À ces fréquences, l'onde réfléchie par la fin de la chambre revient en opposition de phase parfaite avec l'onde entrante. -
Les "Trous" de Fréquence (Transparence) :
Le silencieux devient totalement inefficace (\(TL = 0 \text{ dB}\)) lorsque \(L\) est un multiple de la demi-longueur d'onde : \(L = n \frac{\lambda}{2}\). À ces fréquences, la chambre entre en résonance "demi-onde" et facilite le passage du son au lieu de le bloquer.
-
Condition d'Efficacité Maximale (Résonance Quart d'Onde) :
-
⚠️
Point Clé 3 : Les Limites de Validité
Les formules utilisées dans cet exercice reposent sur l'hypothèse des Ondes Planes (propagation 1D). Cette hypothèse tombe dès que la fréquence augmente.
-
Fréquence de coupure \(f_c\) :
Dès que la longueur d'onde devient comparable au diamètre de la chambre (\(\lambda \approx 1.7 d_2\)), des modes transverses (radiaux) apparaissent. L'onde rebondit "en biais" sur les parois et la performance chute drastiquement.
Règle du pouce : Le modèle n'est fiable que pour \(f < \frac{0.586 c}{d_2}\). - Effet de l'écoulement : Si le silencieux est placé sur un échappement moteur, la vitesse des gaz (\(V\)) n'est pas nulle. Le nombre d'onde effectif change (\(k_{\pm} = k / (1 \pm M)\)), décalant les fréquences de résonance vers le haut ou le bas selon le sens du courant.
-
Fréquence de coupure \(f_c\) :
Dès que la longueur d'onde devient comparable au diamètre de la chambre (\(\lambda \approx 1.7 d_2\)), des modes transverses (radiaux) apparaissent. L'onde rebondit "en biais" sur les parois et la performance chute drastiquement.
🎛️ Simulateur Interactif : Conception & Performance
Concevez votre silencieux en ajustant la géométrie et visualisez instantanément sa réponse acoustique.
1. Géométrie (Paramètres)
2. Vue en Coupe (Dynamique)
Représentation à l'échelle (normalisée)
3. Performance Acoustique (TL)
📝 Quiz final : Testez vos connaissances
Répondez à toutes les questions ci-dessous pour vérifier votre compréhension du dimensionnement acoustique.
1. Quel est le principe fondamental de fonctionnement d'un silencieux réactif (chambre d'expansion) ?
2. Si je double la longueur \(L\) de la chambre, comment évolue la première fréquence d'atténuation maximale ?
Exemple intuitif : Un tuyau d'orgue plus long produit un son plus grave. Ici, une chambre plus longue permet de traiter des fréquences plus basses.
3. On passe d'un conduit de diamètre \(10 \text{ cm}\) à une chambre de diamètre \(20 \text{ cm}\). Quel est le taux d'expansion \(m\) ?
La formule est \(m = (d_2/d_1)^2\). Ici, \(d_2/d_1 = 20/10 = 2\). Donc \(m = 2^2 = 4\). C'est une erreur classique à éviter absolument.
4. Pourquoi ce modèle de calcul devient-il invalide à très haute fréquence ?
5. Que se passe-t-il lorsque la longueur de la chambre est exactement égale à une demi-longueur d'onde (\(L = \lambda/2\)) ?
📚 Glossaire Technique Approfondi
- Impédance Acoustique Spécifique (\(Z_s\))
-
C'est la résistance intrinsèque qu'oppose un milieu à la mise en mouvement de ses particules par une onde sonore. Elle est définie par le produit de la masse volumique du fluide (\(\rho\)) et de la célérité du son (\(c\)).
Formule : \(Z_s = \rho \cdot c\) (en Pa·s/m ou Rayls).
Importance : Dans un silencieux, c'est la variation brusque de cette impédance (liée au changement de section \(S\)) qui provoque la réflexion de l'onde. Une onde qui passe d'un petit tuyau à une grande chambre "voit" une impédance de rayonnement différente, ce qui force une partie de l'énergie à rebrousser chemin.
- Onde Plane (Hypothèse de base)
-
Modèle théorique où les fronts d'onde (surfaces d'égale pression) sont des plans parallèles, perpendiculaires à la direction de propagation. Cela signifie que la pression acoustique est uniforme sur toute la section du tuyau.
Validité : Cette hypothèse n'est vraie que pour les basses fréquences. Dès que la longueur d'onde \(\lambda\) devient comparable aux dimensions transversales du conduit (diamètre \(d\)), des modes transverses complexes apparaissent et l'onde n'est plus plane.
Limite : \(f < \frac{0.586 c}{d}\) (Fréquence de coupure du premier mode transverse dans un tube circulaire).
- Perte par Transmission (TL - Transmission Loss)
-
Indicateur de performance intrinsèque d'un élément acoustique, indépendant de l'environnement (source ou terminaison). Il correspond à la différence logarithmique entre la puissance acoustique incidente (\(W_{inc}\)) et la puissance acoustique transmise (\(W_{trans}\)).
Formule : \(TL = 10 \log_{10}\left(\frac{W_{inc}}{W_{trans}}\right)\) dB.
Note : Ne pas confondre avec l'Insertion Loss (IL), qui mesure la différence de niveau sonore en un point précis avec et sans le silencieux (ce qui dépend de tout le réseau).
- Silencieux Réactif (vs Dissipatif)
-
Type de silencieux qui fonctionne en réfléchissant l'énergie sonore vers la source grâce à des changements de géométrie (chambres, chicanes, résonateurs de Helmholtz). Il ne contient pas de matériau absorbant (laine de roche, mousse).
Avantages : Robuste, hygiénique (pas de fibres), efficace aux basses fréquences.
Inconvénients : Bandes passantes étroites (efficace seulement à certaines fréquences), crée des contre-pressions aérauliques.
- Nombre d'Onde (\(k\))
-
Grandeur fondamentale représentant la "fréquence spatiale" de l'onde. Si la fréquence \(f\) compte le nombre de cycles par seconde, le nombre d'onde \(k\) compte le nombre de radians de phase par mètre parcouru.
Relation : \(k = \frac{2\pi}{\lambda} = \frac{\omega}{c}\).
Sens physique : Plus \(k\) est élevé, plus la phase change vite dans l'espace (longueur d'onde courte, son aigu).
- Onde Stationnaire
-
Phénomène d'interférence résultant de la superposition de deux ondes de même fréquence se propageant en sens inverse (l'onde incidente et l'onde réfléchie par la sortie de la chambre).
Cela crée une figure vibratoire immobile dans l'espace, avec des zones fixes de pression maximale (ventres) et de pression nulle (nœuds). C'est ce phénomène qui bloque le transfert d'énergie vers la sortie à la fréquence de résonance.
Feedback
Chargement...





0 commentaires