Distinction entre la Localisation Sonore
Contexte : La scène auditive 3D.
Notre cerveau est capable de construire une représentation tridimensionnelle de notre environnement sonore à partir des signaux captés par nos deux oreilles. Ce processus, appelé localisation sonore, semble simple mais repose sur une analyse complexe d'indices subtils. Cet exercice explore la distinction fondamentale entre la psychoacoustiqueBranche de la psychophysique qui étudie les relations entre les stimuli sonores et la sensation et perception auditive., qui étudie les indices physiques et la manière dont nous les traitons, et la perceptionProcessus cognitif par lequel le cerveau interprète les sensations auditives pour leur donner un sens, comme la position d'une source sonore., qui est l'interprétation subjective et cognitive de ces indices.
Remarque Pédagogique : Comprendre cette distinction est crucial. Cela permet de saisir pourquoi des situations acoustiques physiquement identiques peuvent être perçues différemment et comment notre cerveau résout les ambiguïtés pour créer une expérience auditive cohérente.
Objectifs Pédagogiques
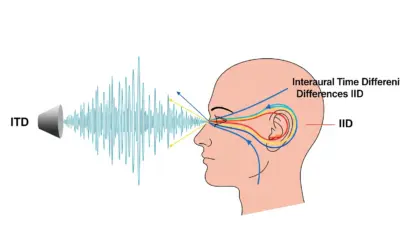
- Distinguer les deux principaux indices binauraux : la différence de temps interaurale (ITD) et la différence de niveau interaurale (ILD).
- Comprendre le concept du cône de confusion et son impact sur la localisation.
- Expliquer comment les indices spectraux et les mouvements de la tête aident à résoudre les ambiguïtés de localisation.
- Identifier l'influence des facteurs cognitifs (comme la vision) sur la perception de l'espace sonore.
Données de l'étude
Conditions de l'Expérience
| Caractéristique | Valeur |
|---|---|
| Environnement d'écoute | Chambre anéchoïque (sans réverbération) |
| Type de son | Tonalité pure |
| Position de la source (azimut) | Variable |
Indices Binauraux pour la Localisation Sonore
| Indice Psychoacoustique | Description | Fréquences Efficaces | Unité |
|---|---|---|---|
| ITD (Diff. de Temps) | Le son arrive à une oreille avant l'autre. | Basses fréquences (< 1500 Hz) | microsecondes (µs) |
| ILD (Diff. de Niveau) | La tête crée une "ombre" qui atténue le son pour l'oreille la plus éloignée. | Hautes fréquences (> 1500 Hz) | décibels (dB) |
Questions à traiter
- Une source sonore est placée à un azimut de 30° sur la droite. En utilisant un modèle simplifié où la distance entre les oreilles est de 20 cm et la vitesse du son de 343 m/s, estimez la différence de temps interaurale (ITD).
- Expliquez physiquement pourquoi l'indice ILD est beaucoup plus efficace pour localiser un son aigu (ex: 4000 Hz) qu'un son grave (ex: 200 Hz).
- Un son est perçu comme venant de "devant, légèrement à droite". Quelles autres positions pourraient produire des indices ITD et ILD quasiment identiques ? Comment appelle-t-on cet ensemble de points ?
- Quelle action simple le sujet peut-il réaliser pour lever l'ambiguïté décrite dans la question 3 ? Expliquez brièvement le mécanisme psychoacoustique sous-jacent.
- On présente au sujet une vidéo d'une personne parlant face à lui (azimut 0°), mais le son provient d'un haut-parleur situé à 45° à droite. Où le sujet va-t-il percevoir l'origine du son, et comment nomme-t-on cet effet de perception multimodale ?
Les bases de la Localisation Sonore
Pour situer une source sonore dans l'espace, notre système auditif s'appuie principalement sur trois types d'indices.
1. Les Indices Binauraux (ITD & ILD)
Ces indices exploitent le fait que nous avons deux oreilles.
- Différence de Temps Interaurale (ITD) : Pour toute source qui n'est pas parfaitement en face ou derrière, le son atteint une oreille une fraction de seconde avant l'autre. Le cerveau peut détecter des décalages de l'ordre de 10 microsecondes. C'est l'indice principal pour les basses fréquences.
- Différence de Niveau Interaurale (ILD) : La tête agit comme un obstacle acoustique. Pour les hautes fréquences (dont la longueur d'onde est plus courte que la taille de la tête), l'oreille la plus éloignée de la source reçoit un son moins intense. C'est l'indice dominant pour les hautes fréquences.
2. Les Indices Spectraux (ou Monauraux)
Les formes complexes de notre oreille externe (le pavillon) filtrent le son différemment selon sa direction d'origine, notamment sur l'axe vertical (élévation). Ces "colorations" spectrales, apprises par notre cerveau, nous aident à savoir si un son vient d'en haut, d'en bas, de devant ou de derrière, levant ainsi une partie des ambiguïtés des indices binauraux.
Correction : Distinction entre la Localisation Sonore
Question 1 : Estimer l'ITD pour une source à 30°
Principe (le concept physique)
Le calcul de la Différence de Temps Interaurale (ITD) repose sur un principe géométrique simple : un son provenant d'une source décentrée parcourt une distance légèrement plus longue pour atteindre l'oreille la plus éloignée que l'oreille la plus proche. Notre cerveau est capable de mesurer ce minuscule décalage temporel pour déterminer la direction horizontale du son.
Mini-Cours (approfondissement théorique)
Ce traitement neurologique s'effectue principalement dans le tronc cérébral, au niveau d'un groupe de neurones appelé le complexe olivaire supérieur (en particulier l'olive supérieure médiane - MSO). Le MSO contient des "détecteurs de coïncidence" qui s'activent lorsque les impulsions nerveuses des deux oreilles arrivent simultanément. Le neurone qui s'active indique le décalage temporel et donc l'angle de la source sonore, selon un principe connu sous le nom de modèle de Jeffress.
Remarque Pédagogique (le conseil du professeur)
Avant tout calcul, visualisez toujours la situation. Imaginez la tête vue de dessus, la source sonore, et les trajets des ondes sonores vers chaque oreille. Ce simple dessin mental ou sur papier vous aidera à comprendre pourquoi il y a une différence de chemin et à appliquer correctement la trigonométrie sans vous tromper de signe ou d'angle.
Normes (la référence réglementaire)
En psychoacoustique, il n'y a pas de "normes" de construction, mais des modèles physiques et mathématiques standardisés. Le calcul présenté ici est basé sur un modèle géométrique simplifié (modèle de Woodworth) qui considère la tête comme une sphère parfaite. C'est une approximation très utilisée pour les calculs de base.
Formule(s) (l'outil mathématique)
Le modèle simplifié approxime la différence de chemin (\(\Delta d\)) à l'aide de la trigonométrie :
Formule de la différence de chemin
L'ITD est alors cette distance divisée par la vitesse du son (\(c\)) :
Formule de la Différence de Temps Interaurale (ITD)
Hypothèses (le cadre du calcul)
Pour que notre modèle soit applicable, nous posons plusieurs hypothèses simplificatrices :
- La tête est une sphère parfaite, sans l'influence du nez ou des pavillons d'oreille.
- La source sonore est suffisamment éloignée ("champ lointain") pour que les ondes sonores soient considérées comme des ondes planes parallèles lorsqu'elles atteignent la tête.
- Le milieu (l'air) est homogène, et la vitesse du son est constante.
Donnée(s) (les chiffres d'entrée)
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Angle de la source | \(\theta\) | 30 | \(\text{degrés}\) |
| Distance interaurale | \(d\) | 0.2 | \(\text{m}\) |
| Vitesse du son | \(c\) | 343 | \(\text{m/s}\) |
Astuces (Pour aller plus vite)
Pour vérifier rapidement un ordre de grandeur : l'ITD maximale pour une tête humaine est d'environ 650-700 µs (à 90°). Comme \(\sin(30^\circ) = 0.5\), on peut s'attendre à une ITD d'environ la moitié de la valeur maximale, soit autour de 325-350 µs. Si votre résultat est très différent, vérifiez vos unités ou votre calcul.
Schéma (Avant les calculs)
Le schéma ci-dessous montre la géométrie du problème, avec la différence de chemin Δd que le son doit parcourir en plus pour atteindre l'oreille gauche.
Géométrie pour le calcul de l'ITD
Calcul(s) (l'application numérique)
Calcul de la différence de chemin effective
Calcul de l'ITD en secondes
Conversion de l'ITD en microsecondes
Schéma (Après les calculs)
Le résultat peut être visualisé sur une courbe théorique de l'ITD. Le graphique montre que notre valeur calculée se positionne correctement sur la sinusoïde qui représente l'ITD en fonction de l'angle de la source.
Courbe de l'ITD en fonction de l'Angle
Réflexions (l'interprétation du résultat)
Une valeur d'environ 292 µs est un décalage temporel extrêmement court, mais il est largement suffisant pour que notre système nerveux le détecte et l'interprète comme une direction. Ce calcul simple démontre la précision temporelle remarquable de notre audition.
Points de vigilance (les erreurs à éviter)
Les deux erreurs les plus communes sont : 1) Oublier de convertir la distance interaurale de cm en m. 2) Se tromper dans la conversion du résultat final de secondes en microsecondes (un facteur de 1 million, soit 10⁶).
Points à retenir (permettre a l'apprenant de maitriser la question)
Synthèse de la Question 1 :
- Concept Clé : L'ITD est la différence de temps d'arrivée du son, causée par la différence de chemin.
- Formule Essentielle : \(\text{ITD} = (d \cdot \sin\theta) / c\).
- Point de Vigilance Majeur : Cohérence des unités (mètres, secondes) avant le calcul final.
Le saviez-vous ? (la culture de l'ingénieur)
Certains animaux, comme la chouette effraie, ont une audition encore plus spécialisée. Leurs oreilles sont positionnées de manière asymétrique en hauteur, ce qui leur permet de créer une ITD sur l'axe vertical et de localiser leurs proies dans l'obscurité la plus totale avec une précision redoutable.
FAQ (pour lever les doutes)
Résultat Final (la conclusion chiffrée)
A vous de jouer (pour verifier la comprehension de l'etudiant parrapport a la question)
Excellent travail ! Pour vérifier votre compréhension, recalculez l'ITD pour une source sonore placée à 60°.
Question 2 : Efficacité de l'ILD selon la fréquence
Principe (le concept physique)
L'efficacité de la Différence de Niveau Interaurale (ILD) est gouvernée par la diffraction. Un son se comporte comme une onde. Si sa longueur d'onde est bien plus grande que l'obstacle (la tête), l'onde le contourne facilement. Si sa longueur d'onde est plus petite, l'obstacle bloque l'onde et crée une "ombre" acoustique derrière lui.
Mini-Cours (approfondissement théorique)
La différence de niveau est traitée par un autre noyau du tronc cérébral, l'olive supérieure latérale (LSO). Les neurones du LSO reçoivent des signaux excitateurs de l'oreille du même côté (ipsilatérale) et des signaux inhibiteurs de l'oreille opposée (contralatérale). La différence d'intensité de ces signaux détermine le niveau d'activation du neurone, codant ainsi l'ILD et donc la position de la source sonore.
Remarque Pédagogique (le conseil du professeur)
Utilisez l'analogie des vagues et d'un poteau dans l'eau. Une longue houle (basse fréquence) va envelopper le poteau sans être perturbée. Des petites vaguelettes (haute fréquence) seront bloquées par le poteau, créant une zone calme derrière lui. La tête est le poteau, le son est les vagues.
Normes (la référence réglementaire)
Il n'y a pas de norme, mais ce phénomène est quantifié précisément par les Fonctions de Transfert relatives à la Tête (HRTF). Ce sont des filtres acoustiques mesurés pour chaque individu (ou standardisés) qui décrivent comment le son est modifié par la tête, le torse et les oreilles pour chaque direction de l'espace. Les HRTF capturent l'ILD et l'ITD pour toutes les fréquences.
Formule(s) (l'outil mathématique)
La formule clé est celle qui lie la longueur d'onde (\(\lambda\)), la vitesse du son (\(c\)) et la fréquence (\(f\)) :
Relation Longueur d'onde - Fréquence
Il n'y a pas de formule simple pour l'ILD car elle dépend de processus de diffraction complexes, mais on la compare à la taille de l'obstacle.
Hypothèses (le cadre du calcul)
Nous comparons la longueur d'onde calculée au diamètre approximatif de la tête humaine.
- Le diamètre moyen de la tête est considéré comme étant d'environ 20 cm (0.2 m).
- La vitesse du son dans l'air est de 343 m/s.
Donnée(s) (les chiffres d'entrée)
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Fréquence du son grave | \(f_{\text{grave}}\) | 200 | \(\text{Hz}\) |
| Fréquence du son aigu | \(f_{\text{aigu}}\) | 4000 | \(\text{Hz}\) |
Astuces (Pour aller plus vite)
La fréquence de transition se situe autour de 1500 Hz. En dessous, pensez "temps" (ITD). Au-dessus, pensez "intensité" (ILD). C'est le cœur de la "Théorie Duplex" de la localisation sonore.
Schéma (Avant les calculs)
Ce schéma illustre la diffraction des ondes sonores autour d'une tête schématisée en fonction de leur longueur d'onde.
Diffraction et Ombre Acoustique
Calcul(s) (l'application numérique)
Calcul de la longueur d'onde pour le son grave (200 Hz)
Calcul de la longueur d'onde pour le son aigu (4000 Hz)
Schéma (Après les calculs)
Ce graphique illustre la "Théorie Duplex" : l'ILD est négligeable à basses fréquences (où l'ITD domine) et devient un indice de plus en plus fort à mesure que la fréquence augmente, dépassant le seuil de pertinence (~1-2 dB) dans la zone de transition.
Efficacité de l'ILD en fonction de la Fréquence
Réflexions (l'interprétation du résultat)
La longueur d'onde du son grave (1.72 m) est presque 9 fois plus grande que le diamètre de la tête (~0.2 m). Le son l'ignore presque complètement. La longueur d'onde du son aigu (8.6 cm) est plus de deux fois plus petite que la tête, qui devient un obstacle très efficace, créant une ombre et donc un ILD fort et fiable pour la localisation.
Points de vigilance (les erreurs à éviter)
Ne pas simplement dire "les sons graves contournent les obstacles". Soyez précis en liant ce phénomène à la comparaison entre la longueur d'onde et la taille de l'obstacle. C'est cette comparaison qui est au cœur du raisonnement physique.
Points à retenir (permettre a l'apprenant de maitriser la question)
Synthèse de la Question 2 :
- Concept Clé : La diffraction dépend du rapport \(\lambda / D\) (longueur d'onde / taille de l'obstacle).
- Règle : Si \(\lambda \gg D\), diffraction importante (pas d'ombre, ILD faible). Si \(\lambda \ll D\), diffraction faible (ombre, ILD forte).
- Application : Les basses fréquences ont de grandes \(\lambda\), les hautes fréquences ont de petites \(\lambda\).
Le saviez-vous ? (la culture de l'ingénieur)
Ce principe est fondamental en ingénierie acoustique. C'est pourquoi les barrières anti-bruit le long des autoroutes sont efficaces pour bloquer le son aigu des pneus sur la route, mais beaucoup moins pour le bruit grave des moteurs, dont les grandes longueurs d'onde "passent par-dessus" l'obstacle.
FAQ (pour lever les doutes)
Résultat Final (la conclusion chiffrée)
A vous de jouer (pour verifier la comprehension de l'etudiant parrapport a la question)
Un animal a une toute petite tête (ex: 5 cm de diamètre). Serait-il plus performant pour localiser les sons aigus ou les sons graves en utilisant l'ILD ?
Question 3 : Ambiguïté de localisation et Cône de Confusion
Principe
Pour un angle donné par rapport à l'axe interaural, il n'existe pas un seul point dans l'espace, mais un ensemble de points qui génèrent la même paire d'indices ITD et ILD. Le cerveau ne peut donc pas distinguer ces positions en se basant uniquement sur ces deux indices.
Mini-Cours
Cet ensemble de points forme une surface conique avec l'axe interaural comme axe de symétrie. On l'appelle le cône de confusion. Toutes les sources sonores situées sur la surface de ce cône produiront les mêmes ITD et ILD, créant une ambiguïté de localisation (devant/derrière, haut/bas).
Donnée(s) (les chiffres d'entrée)
Les données pour cette question sont conceptuelles : nous partons d'une paire d'indices ITD/ILD donnée qui correspond à la perception "devant, légèrement à droite".
Schéma (Avant les calculs)
Avant de comprendre le concept du cône, l'ambiguïté se présente comme une simple question : si le son n'est pas au centre, est-il devant ou derrière ?
Ambiguïté de Localisation (Devant vs. Derrière)
Schéma (Après les calculs)
La résolution conceptuelle montre que l'ambiguïté ne se limite pas à devant/derrière, mais forme une surface conique.
Le Cône de Confusion
Réflexions
Si un son est perçu "devant, légèrement à droite", cela signifie qu'il se trouve sur un cône de confusion. Les autres positions ambiguës incluent "derrière, légèrement à droite", mais aussi "en haut, à droite" et "en bas, à droite" au même angle par rapport à l'axe des oreilles. Sans informations supplémentaires, le cerveau a du mal à faire la différence.
Résultat Final
Question 4 : Résoudre l'ambiguïté du cône de confusion
Principe
Le cône de confusion n'est un problème que pour une tête immobile. Le moindre mouvement de la tête change la relation géométrique entre la source et les oreilles, fournissant au cerveau les informations manquantes pour lever l'ambiguïté.
Mini-Cours
Lorsque nous tournons la tête, les indices ITD et ILD changent de manière dynamique. Par exemple, si une source ambiguë (devant ou derrière) est en réalité devant, une légère rotation de la tête vers la droite augmentera l'ITD. Si elle était derrière, le même mouvement le diminuerait. Le cerveau est extraordinairement doué pour analyser ces changements dynamiques et "casser" la symétrie du cône de confusion, localisant ainsi la source avec précision.
Donnée(s) (les chiffres d'entrée)
La donnée est la situation d'ambiguïté identifiée à la question 3.
Schéma (Avant les calculs)
Situation Statique Ambiguë
Schéma (Après les calculs)
Résolution par Mouvement de la Tête
Astuces
C'est un réflexe quasi-inconscient. Lorsque vous entendez un son inattendu, votre premier instinct est souvent de tourner la tête dans sa direction. Ce n'est pas seulement pour mieux voir, c'est avant tout pour mieux localiser le son !
Le saviez-vous ?
Les animaux dotés d'oreilles mobiles, comme les chats ou les chiens, font la même chose mais de manière encore plus efficace. En orientant leurs pavillons, ils modifient les indices spectraux et binauraux pour une localisation ultra-précise de leur proie ou d'un danger potentiel.
Résultat Final
Question 5 : Influence de la vision sur la perception auditive
Principe
La perception n'est pas un traitement isolé de chaque sens. Le cerveau fusionne en permanence les informations provenant de différentes modalités sensorielles (vue, ouïe, toucher) pour créer une interprétation unifiée et cohérente du monde. En cas de conflit, un sens peut en dominer un autre.
Mini-Cours
Ce phénomène est connu sous le nom d'effet ventriloque ou de capture visuelle. Lorsque des informations auditives et visuelles contradictoires mais plausibles sont présentées simultanément, le cerveau a tendance à faire davantage confiance à la localisation visuelle, qui est généralement plus précise. Il "déplace" alors la perception de la source sonore pour la faire coïncider avec la source visuelle.
Donnée(s) (les chiffres d'entrée)
| Stimulus | Position Physique (Azimut) |
|---|---|
| Vidéo (visuel) | 0° (en face) |
| Haut-parleur (auditif) | 45° (à droite) |
Schéma (Avant les calculs)
Configuration Physique des Stimuli
Schéma (Après les calculs)
Localisation Perçue
Réflexions
Cet effet est omniprésent. Au cinéma, le son provient de haut-parleurs sur les côtés de la salle, mais vous percevez la voix des acteurs comme venant directement de leur bouche à l'écran. Votre cerveau recalibre en permanence votre perception auditive pour qu'elle corresponde à ce que vous voyez.
Points à retenir
La perception de l'espace n'est pas seulement auditive ; c'est une construction multimodale. La localisation sonore perçue n'est pas toujours la localisation physique réelle, elle peut être fortement influencée par des indices visuels ou même des attentes cognitives.
Résultat Final
Outil Interactif : Simulateur d'Indices Binauraux
Utilisez les curseurs pour modifier l'angle de la source sonore et la taille de la tête, et observez comment les indices ITD et ILD (modèles simplifiés) sont affectés. Le graphique montre la variation de l'ITD en fonction de l'angle.
Paramètres d'Entrée
Résultats Clés (Estimations)
Quiz Final : Testez vos connaissances
1. Quel indice de localisation est le plus important pour un son très grave comme un coup de tonnerre lointain ?
2. Le "cône de confusion" se réfère à :
3. Pour déterminer si un son vient d'en haut ou d'en bas, le cerveau se base principalement sur :
4. L'effet ventriloque démontre que :
5. Si vous augmentez la distance entre vos oreilles (par exemple, si vous étiez une créature avec une très grosse tête), quel effet cela aurait-il sur l'ITD pour une source sonore donnée ?
Glossaire
- Psychoacoustique
- Branche de la science qui étudie la perception subjective des sons par l'être humain, en lien avec leurs caractéristiques physiques (fréquence, intensité, etc.).
- Perception
- Processus cognitif d'interprétation et de compréhension des informations sensorielles. En audition, c'est la "prise de conscience" de la scène sonore.
- ITD (Interaural Time Difference)
- Différence de temps d'arrivée d'un son entre les deux oreilles. C'est un indice majeur pour la localisation sur le plan horizontal, surtout en basses fréquences.
- ILD (Interaural Level Difference)
- Différence d'intensité (niveau sonore) d'un son entre les deux oreilles, causée par l'ombre acoustique de la tête. C'est un indice majeur pour les hautes fréquences.
- Cône de Confusion
- Ensemble de points dans l'espace qui produisent la même paire d'indices ITD et ILD, créant une ambiguïté de localisation que le cerveau doit résoudre par d'autres moyens.
- Effet Ventriloque
- Phénomène de perception multimodale où la localisation perçue d'une source sonore est déplacée pour correspondre à la position d'une source visuelle présentée simultanément.
D'autres exercices de Psychoacoustique:

0 commentaires