Localisation Sonore : Rôle des Indices de Temps (ITD) et d’Intensité (IID)
Contexte : La PsychoacoustiqueBranche de la science qui étudie la perception subjective des sons par l'être humain..
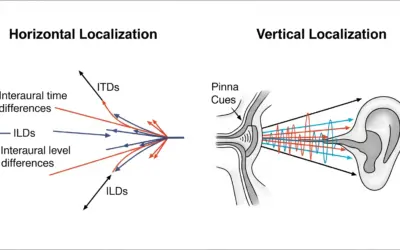
La capacité à localiser une source sonore dans notre environnement est un aspect fondamental de notre perception auditive. Cette compétence, appelée localisation sonore, repose sur la manière dont notre cerveau analyse et interprète les infimes différences entre les sons qui parviennent à nos deux oreilles. Cet exercice se concentre sur les deux indices binauraux principaux : la différence de temps interaurale (ITD) et la différence d'intensité interaurale (IID), concepts clés de la "Théorie Duplex" de Lord Rayleigh.
Remarque Pédagogique : Cet exercice vous permettra de comprendre comment les lois de la physique (propagation du son, effet d'ombre) se combinent avec l'anatomie humaine pour créer des indices exploitables par notre système nerveux, nous offrant ainsi une perception tridimensionnelle du monde sonore.
Objectifs Pédagogiques
- Comprendre le concept d'indice interaural de temps (ITD) et son rôle pour les basses fréquences.
- Comprendre le concept d'indice interaural d'intensité (IID) et son rôle pour les hautes fréquences.
- Appliquer des modèles simplifiés pour estimer la valeur de l'ITD en fonction de la position d'une source.
- Expliquer la Théorie Duplex et ses limites, comme le cône de confusion.
Données de l'étude
Modèle Sphérique de la Tête
| Paramètre | Description | Valeur | Unité |
|---|---|---|---|
| c | Vitesse du son dans l'air (à 20°C) | 343 | m/s |
| r | Rayon moyen de la tête modélisée | 0.0875 | m |
Questions à traiter
- Calculez la différence de temps interaurale (ITD) maximale que peut percevoir un auditeur.
- Calculez l'ITD pour une source sonore située à un angle de 45°.
- Expliquez, en utilisant la notion de longueur d'onde, pourquoi l'indice d'intensité (IID) est un indice pertinent principalement pour les hautes fréquences.
- Décrivez ce qu'est le "cône de confusion" et comment notre système auditif parvient généralement à lever cette ambiguïté.
- Une source émet un son pur à 2500 Hz. L'ITD mesuré est de 0.4 ms. Le cerveau peut-il utiliser cette information de manière fiable ? Justifiez votre réponse en comparant l'ITD à la période du signal.
Les bases sur la Localisation Binaurale
Notre cerveau localise les sons en se basant sur deux indices principaux, qui forment la Théorie Duplex.
1. Indice Interaural de Temps (ITD)
L'ITD est la différence de temps d'arrivée d'un son entre les deux oreilles. Si une source est sur notre droite, le son atteint l'oreille droite avant l'oreille gauche. Ce délai est maximal pour les sons venant directement de côté (90°) et nul pour les sons venant de face ou de derrière. C'est l'indice principal pour les basses fréquences (< 1500 Hz). Un modèle simplifié pour une tête sphérique donne :
\[ \text{ITD} = \frac{r}{c} (\theta + \sin\theta) \]
Où \(r\) est le rayon de la tête, \(c\) la vitesse du son, et \(\theta\) est l'angle de la source en radians par rapport à l'axe frontal.
2. Indice Interaural d'Intensité (IID)
L'IID est la différence de niveau d'intensité (volume) d'un son entre les deux oreilles. La tête agit comme un obstacle acoustique, créant un "effet d'ombre" pour l'oreille la plus éloignée de la source. Cet effet est négligeable pour les sons dont la longueur d'onde est grande par rapport à la taille de la tête (basses fréquences), mais il devient très important pour les sons à courte longueur d'onde (hautes fréquences, > 1500 Hz).
Correction : Rôle des Indices de Temps (ITD) et d’Intensité (IID)
Question 1 : Calculez la différence de temps interaurale (ITD) maximale.
Principe
L'ITD maximal se produit lorsque la différence de chemin que le son doit parcourir pour atteindre les deux oreilles est la plus grande possible. Physiquement, cela correspond à la situation où une source sonore se trouve directement sur le côté de l'auditeur (à 90° par rapport à l'avant), maximisant la distance que le son doit "contourner" la tête pour atteindre l'oreille la plus éloignée.
Mini-Cours
La différence de temps (\(\Delta t\)) est directement liée à la différence de distance parcourue (\(\Delta d\)) par une onde se propageant à une vitesse constante \(c\), via la relation \(\Delta t = \Delta d / c\). Dans notre cas, \(\Delta d\) est la différence de chemin acoustique entre la source et chaque oreille. Le modèle de tête sphérique est une approximation (modèle de Woodworth) qui simplifie ce calcul de chemin.
Remarque Pédagogique
Pour trouver la valeur maximale d'une fonction, on cherche généralement les conditions qui maximisent ses variables. Ici, la fonction ITD(\(\theta\)) est croissante entre 0° et 90°. La valeur maximale sera donc logiquement atteinte à l'extrémité de cet intervalle, c'est-à-dire pour \(\theta = 90°\).
Normes
Il n'y a pas de "norme" réglementaire comme en BTP. La "norme" ici est le modèle physique utilisé. Nous nous basons sur le modèle de tête sphérique de Woodworth (1938), qui est une référence académique standard pour une première approximation de l'ITD.
Formule(s)
Formule de l'Indice Interaural de Temps (ITD)
Hypothèses
Le calcul repose sur plusieurs simplifications importantes :
- La tête est une sphère parfaite et rigide.
- La source sonore est suffisamment éloignée (onde plane).
- L'environnement est anéchoïque (pas de réflexions sonores).
- Les effets du pavillon de l'oreille, du torse et des épaules sont ignorés.
Donnée(s)
Les valeurs d'entrée pour trouver le cas maximal :
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Angle azimutal (cas max) | \(\theta\) | 90 | degrés |
| Rayon de la tête | \(r\) | 0.0875 | m |
| Vitesse du son | \(c\) | 343 | m/s |
Astuces
Pour une vérification rapide, on peut approximer la différence de chemin maximale par le diamètre de la tête, plus un petit trajet pour la contourner, soit un peu plus que \(2r\). Une approximation simple est \(\Delta d \approx \pi r\). Le temps serait alors \(t \approx \pi r / c = (\pi \times 0.0875) / 343 \approx 0.8\) ms. Cela donne un ordre de grandeur pour valider notre calcul plus précis.
Schéma (Avant les calculs)
Configuration pour l'ITD Maximal (Source à 90°)
Calcul(s)
Étape 1 : Conversion de l'angle en radians
Étape 2 : Calcul de l'ITD maximal
Schéma (Après les calculs)
Position du Résultat sur la Courbe ITD(θ)
Réflexions
Le résultat est souvent exprimé en millisecondes (ms). Une valeur de \(6.556 \times 10^{-4}\) secondes équivaut à environ 0.656 ms. Cette valeur représente le délai maximal que notre cerveau peut détecter. C'est une durée extrêmement courte, démontrant l'incroyable sensibilité temporelle de notre système auditif.
Points de vigilance
L'erreur la plus commune est d'oublier de convertir l'angle de degrés en radians avant de l'injecter dans la formule trigonométrique. La plupart des fonctions sinus et la formule elle-même sont définies pour des angles en radians. Utiliser 90° directement donnerait un résultat complètement erroné.
Points à retenir
Pour maîtriser cette question, retenez que :
- L'ITD est maximal à 90°.
- La formule \(\text{ITD} = (r/c)(\theta + \sin\theta)\) est un modèle clé.
- La conversion degrés vers radians (\(\theta_{\text{rad}} = \theta_{\text{deg}} \times \pi/180\)) est une étape cruciale.
Le saviez-vous ?
Certains animaux, comme les chouettes effraies, sont des maîtres de la localisation sonore. Leurs oreilles sont asymétriques en hauteur, ce qui leur permet de créer un "ITD vertical" en plus de l'ITD horizontal, leur donnant une carte sonore 3D ultra-précise pour chasser dans l'obscurité totale.
FAQ
Résultat Final
A vous de jouer
En utilisant les mêmes données, quel serait l'ITD maximal si la tête était plus petite, avec un rayon de 0.08 m ?
Question 2 : Calculez l'ITD pour une source sonore située à un angle de 45°.
Principe
Le principe physique reste le même : le son parcourt un chemin légèrement plus long pour atteindre l'oreille la plus éloignée. Cependant, avec un angle de 45°, la source est plus proche de l'axe frontal, donc la différence de chemin sera plus petite que dans le cas maximal à 90°, et l'ITD résultant sera plus faible.
Mini-Cours
La fonction ITD(\(\theta\)) n'est pas linéaire. Un angle deux fois plus petit que 90° (soit 45°) ne produit pas un ITD deux fois plus petit. La présence du terme \(\sin\theta\) dans la formule introduit cette non-linéarité, qui reflète la géométrie sphérique de l'interaction onde-tête.
Remarque Pédagogique
Cette question est une application directe de la précédente. L'objectif est de vérifier que vous pouvez appliquer la même méthode en changeant simplement un paramètre d'entrée (l'angle). Assurez-vous d'être systématique : conversion d'unité, puis application numérique.
Normes
Comme pour la question 1, nous nous référons au modèle de tête sphérique de Woodworth comme standard de calcul pour cet exercice académique.
Formule(s)
Formule de l'Indice Interaural de Temps (ITD)
Hypothèses
Le calcul repose sur plusieurs simplifications importantes :
- La tête est une sphère parfaite et rigide.
- La source sonore est suffisamment éloignée (onde plane).
- L'environnement est anéchoïque (pas de réflexions sonores).
- Les effets du pavillon de l'oreille, du torse et des épaules sont ignorés.
Donnée(s)
Les chiffres d'entrée pour ce cas spécifique :
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Angle azimutal | \(\theta\) | 45 | degrés |
| Rayon de la tête | \(r\) | 0.0875 | m |
| Vitesse du son | \(c\) | 343 | m/s |
Astuces
Avant de calculer, attendez-vous à un résultat significativement inférieur à 0.656 ms mais supérieur à 0. Un rapide coup d'œil à la fonction (\(\theta + \sin\theta\)) montre qu'à 45°, elle vaut environ la moitié de sa valeur à 90°, donc on peut s'attendre à un ITD autour de 0.3-0.4 ms. Cela aide à détecter les erreurs de calcul grossières.
Schéma (Avant les calculs)
Configuration pour ITD à 45°
Calcul(s)
Étape 1 : Conversion de l'angle en radians
Étape 2 : Calcul de l'ITD
Schéma (Après les calculs)
Position du Résultat sur la Courbe ITD(θ)
Réflexions
Le résultat de 0.380 ms est, comme prévu, inférieur à l'ITD maximal. Cela illustre comment le cerveau peut potentiellement utiliser la magnitude de l'ITD pour estimer l'angle d'une source sonore : un petit ITD indique une source proche de l'avant, tandis qu'un grand ITD indique une source sur le côté.
Points de vigilance
Vérifiez toujours le mode de votre calculatrice (degrés ou radians). Comme pour la question 1, utiliser 45 directement dans la fonction sinus donnera un résultat incorrect. Assurez-vous que \(\sin(45)\) est calculé sur la base de 45 degrés, mais que le terme \(\theta\) dans la somme est bien la valeur en radians (0.785).
Points à retenir
Le processus de résolution est générique :
- Identifier l'angle \(\theta\).
- Convertir \(\theta\) en radians.
- Appliquer la formule de l'ITD.
Le saviez-vous ?
Les premiers systèmes de "stéréo" inventés à la fin du 19e siècle, comme le "Théâtrophone" de Clément Ader, fonctionnaient en plaçant deux microphones sur une scène, espacés d'environ une tête humaine, pour recréer artificiellement les ITD et IID et donner une impression d'espace aux auditeurs au téléphone.
FAQ
Résultat Final
A vous de jouer
Quel serait l'ITD pour une source sonore située à 30° ?
Question 3 : Expliquez pourquoi l'IID est pertinent surtout pour les hautes fréquences.
Principe
La pertinence de l'IID dépend de la manière dont le son interagit avec la tête. Cette interaction est dictée par la relation entre la taille de la tête et la longueur d'onde (\(\lambda\)) du son.
Formule(s)
Relation Longueur d'onde - Fréquence
Schéma (Après les calculs)
Interaction Onde-Tête selon la Fréquence
Réflexions
Pour les basses fréquences : La longueur d'onde est grande (ex: à 343 Hz, \(\lambda = 1\) m), bien plus grande que le diamètre de la tête (~0.175 m). Le son "contourne" facilement la tête par diffraction. Il n'y a quasiment pas de perte d'intensité. L'IID est donc très faible et inutilisable.
Pour les hautes fréquences : La longueur d'onde est petite (ex: à 10000 Hz, \(\lambda = 3.43\) cm). Elle est plus petite que la tête. La tête agit comme un obstacle, bloquant une partie de l'énergie sonore et créant une "ombre acoustique" du côté opposé. L'oreille dans cette ombre perçoit un son bien moins intense. L'IID est donc important et constitue un indice de localisation très fiable.
Question 4 : Décrivez ce qu'est le "cône de confusion".
Principe
Le cône de confusion représente l'ensemble des points dans l'espace pour lesquels les valeurs d'ITD et d'IID sont identiques. Le cerveau ne peut donc pas distinguer la provenance d'un son parmi ces points en se basant uniquement sur ces deux indices.
Schéma (Après les calculs)
Illustration du Cône de Confusion
Réflexions
Un son provenant d'un point devant vous à 45° vers le haut produira les mêmes ITD et IID qu'un son provenant d'un point derrière vous à 45° vers le bas. Pour résoudre cette ambiguïté, le cerveau utilise principalement deux stratégies :
1. Les micro-mouvements de la tête : En tournant ou inclinant légèrement la tête, même inconsciemment, on modifie la relation géométrique avec la source. Les ITD et IID changent de manière dynamique, et le cerveau utilise cette variation pour déterminer la position correcte.
2. Les indices spectraux : Le pavillon de l'oreille (la partie visible) filtre le son de manière complexe avant qu'il n'atteigne le tympan. Ce filtrage dépend de la direction d'arrivée du son (surtout en élévation). Le cerveau apprend à reconnaître ces "signatures" spectrales pour affiner la localisation.
Question 5 : Un son à 2500 Hz arrive avec un ITD de 0.4 ms. Est-ce fiable ?
Principe
La fiabilité de l'ITD repose sur la capacité du cerveau à comparer sans ambiguïté la phase de l'onde sonore arrivant à chaque oreille. Si le délai de temps (ITD) devient comparable ou supérieur à la durée d'un cycle de l'onde (sa période), le cerveau ne peut plus savoir à quel cycle de l'onde il doit comparer, ce qui rend l'information inutilisable.
Mini-Cours
Ce phénomène est appelé l'ambiguïté de phase. Les neurones spécialisés dans la détection de l'ITD (dans le tronc cérébral) fonctionnent comme des "détecteurs de coïncidence". Pour les basses fréquences, il n'y a qu'une seule coïncidence possible dans la fenêtre de l'ITD max. Pour les hautes fréquences, la période est si courte que plusieurs coïncidences deviennent possibles, créant une confusion. La limite supérieure généralement admise pour une utilisation fiable de l'ITD se situe autour de 1500 Hz.
Remarque Pédagogique
En physique et en ingénierie, il est toujours crucial de comparer les échelles de temps. Ici, la question vous invite à comparer l'échelle de temps de la perception (l'ITD) avec l'échelle de temps du stimulus physique (la période de l'onde). Si ces échelles sont du même ordre de grandeur, il faut s'attendre à des phénomènes d'interférence ou d'ambiguïté.
Normes
Les recherches en psychoacoustique ont établi la fréquence limite d'environ 1500 Hz pour l'utilisation des indices temporels. Au-delà, le mécanisme neuronal de "phase-locking" devient inefficace, et le cerveau transitionne vers l'utilisation de l'IID comme indice principal.
Formule(s)
Formule de la période
Hypothèses
Nous supposons que le système auditif se base sur la comparaison de phase des cycles de l'onde pour mesurer l'ITD et que le signal est un son pur (sinusoïdal).
Donnée(s)
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Fréquence du son | \(f\) | 2500 | Hz |
| ITD mesuré | \(\text{ITD}\) | 0.4 | ms |
Astuces
Une règle simple : si la fréquence \(f > 1/\text{ITD}_{\text{max}}\), il y aura forcément ambiguïté pour certaines positions. Ici, \(1/0.000656 \approx 1524\) Hz. Comme 2500 Hz est bien supérieur à cette fréquence "limite", on sait que l'ITD ne sera pas un indice fiable.
Schéma (Avant les calculs)
Concept d'Ambigüité de Phase
Calcul(s)
Calcul de la période du signal
Comparaison de l'ITD et de la période
Schéma (Après les calculs)
Visualisation de l'Ambigüité de Phase
Réflexions
Lorsque l'ITD est égal à la période, une crête de l'onde arrive à l'oreille gauche en même temps qu'une crête du cycle *précédent* arrive à l'oreille droite. Pour le cerveau, c'est indiscernable d'une situation où l'ITD serait de 0. L'information de temps est donc ambiguë et inutilisable. À cette fréquence de 2500 Hz, le cerveau se fiera quasi exclusivement à l'IID pour localiser le son.
Points de vigilance
Attention aux unités. L'ITD est donné en millisecondes (ms) et la fréquence en Hertz (Hz). Il est indispensable de tout convertir dans la même unité de temps (secondes ou millisecondes) pour pouvoir les comparer valablement. Ici, \(1/2500 = 0.0004\) s, ce qui est bien \(0.4\) ms.
Points à retenir
La clé de cette question est la condition d'ambiguïté de phase :
- Calculer la période \(T = 1/f\).
- Comparer \(T\) à l'ITD.
- Si \(\text{ITD} \ge T/2\), l'indice temporel devient ambigu et donc peu fiable.
Le saviez-vous ?
Le concept d'ambiguïté de phase n'est pas unique à l'acoustique. Il est fondamental dans de nombreux domaines de l'ingénierie des ondes, comme en radar ou en sonar. Les ingénieurs utilisent des techniques de "dépliage de phase" (phase unwrapping) pour résoudre ces ambiguïtés, une tâche que notre cerveau fait intuitivement en changeant de stratégie (passant de l'ITD à l'IID).
FAQ
Résultat Final
A vous de jouer
Le cerveau peut-il utiliser l'ITD de manière fiable pour localiser un son pur à 800 Hz ? Justifiez par le calcul.
Outil Interactif : Simulateur d'ITD
Ce simulateur vous permet de visualiser comment l'indice de temps interaural (ITD) change en fonction de l'angle de la source sonore, en utilisant le modèle de tête sphérique.
Paramètres d'Entrée
Résultats Clés
Quiz Final : Testez vos connaissances
1. Quel est l'indice de localisation sonore principal pour un son grave (ex: 300 Hz) ?
2. L'effet d'ombre de la tête est le plus prononcé pour...
3. La "Théorie Duplex" de la localisation sonore stipule que...
4. Un ITD de 0 ms signifie que la source sonore est probablement...
5. Comment le cerveau résout-il principalement l'ambiguïté du "cône de confusion" ?
Glossaire
- Indice Interaural de Temps (ITD)
- La différence de temps d'arrivée d'un son entre les deux oreilles. C'est un indice majeur pour la localisation des sons de basse fréquence.
- Indice Interaural d'Intensité (IID)
- La différence de niveau de pression acoustique (intensité) d'un son entre les deux oreilles, causée par l'effet d'ombre de la tête. C'est un indice majeur pour la localisation des sons de haute fréquence.
- Théorie Duplex
- Théorie postulant que la localisation sonore dans le plan horizontal est gérée par deux mécanismes : l'ITD pour les basses fréquences et l'IID pour les hautes fréquences.
- Cône de Confusion
- Un ensemble de positions dans l'espace qui produisent des valeurs d'ITD et d'IID identiques, créant une ambiguïté de localisation que le cerveau doit résoudre par d'autres moyens (mouvements de tête, indices spectraux).
- Psychoacoustique
- La science qui étudie la relation entre les stimuli sonores physiques et la sensation et perception psychologique que ces sons produisent.
D’autres exercice de Psychoacoustique:

0 commentaires