Tracé des Courbes Isosoniques en Psychoacoustique
Contexte : La PsychoacoustiqueLa branche de la psychophysique qui étudie la perception subjective des sons par l'être humain. et la perception de la sonie.
L'oreille humaine ne perçoit pas toutes les fréquences sonores avec la même sensibilité. Un son grave de 50 décibels nous semblera beaucoup moins fort qu'un son médium de 50 décibels. Les courbes isosoniques, aussi appelées courbes d'égale sonie, sont des graphiques qui représentent, pour chaque fréquence du spectre audible, le niveau de pression acoustique (en dB SPL) requis pour qu'un son soit perçu avec la même intensité sonore (sonie). Cet exercice vous guidera dans le calcul et le tracé de points d'une de ces courbes fondamentales.
Remarque Pédagogique : Cet exercice vous permettra de comprendre et de visualiser la nature non-linéaire de l'audition humaine. Vous appliquerez une méthode de calcul simple pour construire un outil essentiel en acoustique et en conception audio.
Objectifs Pédagogiques
- Comprendre la différence entre le niveau de pression acoustique (dB SPL) et le niveau de sonie perçue (PhoneUnité du niveau de sonie. Elle est définie par comparaison avec un son de référence de 1000 Hz.).
- Calculer le niveau de pression acoustique correspondant à un niveau de sonie donné pour différentes fréquences.
- Interpréter la forme d'une courbe isosonique et ce qu'elle révèle sur la sensibilité de l'oreille humaine.
Données de l'étude
Conventions de l'Exercice
| Caractéristique | Valeur / Description |
|---|---|
| Niveau de sonie cible | 40 phones |
| Fréquence de référence | 1000 Hz (par définition, 40 phones = 40 dB SPL à 1000 Hz) |
| Norme de référence | ISO 226:2003 (acoustique) |
Axes du graphique à tracer
| Fréquence (f) | Ajustement de sensibilité A(f) | Niveau de Pression Lp (dB SPL) |
|---|---|---|
| 100 Hz | +11.1 dB | À calculer |
| 250 Hz | +3.8 dB | À calculer |
| 1000 Hz | 0 dB | À calculer |
| 4000 Hz | -8.2 dB | À calculer |
Questions à traiter
- Calculez le niveau de pression acoustique (Lp) requis à 100 Hz pour obtenir une sonie perçue de 40 phones.
- Calculez le niveau de pression acoustique (Lp) requis à 250 Hz.
- Confirmez le niveau de pression acoustique (Lp) à la fréquence de référence de 1000 Hz.
- Calculez le niveau de pression acoustique (Lp) requis à 4000 Hz.
- Décrivez la forme générale de la courbe reliant ces points. Qu'indique-t-elle sur la sensibilité de l'oreille dans les basses et hautes fréquences ?
Les bases sur la Psychoacoustique
Pour résoudre cet exercice, il faut comprendre deux concepts clés qui lient la mesure physique d'un son à sa perception humaine.
1. Niveau de Sonie (Phone)
Le niveau de sonie est une mesure subjective de l'intensité d'un son. L'unité est le phone. Par définition, le niveau de sonie en phones est égal au niveau de pression acoustique en décibels (dB SPL) d'un son de référence de 1000 Hz qui est perçu comme ayant la même intensité. Ainsi, un son de 1000 Hz à 60 dB SPL a un niveau de sonie de 60 phones. Un autre son, par exemple à 200 Hz, qui nous semble aussi fort, aura également un niveau de sonie de 60 phones, même si son niveau en dB SPL est différent.
2. Formule de calcul pour l'exercice
Pour simplifier les calculs complexes de la norme ISO 226, nous utiliserons une relation directe. Pour un niveau de sonie cible (ici, 40 phones), le niveau de pression acoustique \(L_p\) à une fréquence \(f\) est donné par l'addition du niveau de sonie et d'un facteur d'ajustement \(A(f)\) qui dépend de la fréquence.
\[ L_p(f) [\text{dB SPL}] = \text{Niveau de Sonie} [\text{phones}] + A(f) [\text{dB}] \]
Correction : Tracé des Courbes Isosoniques
Question 1 : Calcul du Lp à 100 Hz
Principe (le concept physique)
L'objectif est de trouver le niveau de pression acoustique physique (en dB SPL), c'est-à-dire l'intensité réelle de l'onde sonore, nécessaire pour qu'un son grave de 100 Hz soit perçu par l'oreille humaine comme ayant une intensité subjective de 40 phones.
Mini-Cours (approfondissement théorique)
L'oreille humaine n'est pas un capteur linéaire. La cochlée, l'organe de l'audition, répond différemment selon la fréquence du son. Dans les basses fréquences, la membrane basilaire est plus rigide et moins mobile, ce qui signifie qu'il faut une plus grande amplitude de vibration (donc une plus grande pression acoustique) pour stimuler les cellules ciliées avec la même efficacité que dans les fréquences moyennes.
Remarque Pédagogique (le conseil du professeur)
Considérez toujours la fréquence de 1000 Hz comme votre point de repère absolu. Pour toute autre fréquence, demandez-vous : "mon oreille est-elle plus ou moins sensible qu'à 1000 Hz ?". Si elle est moins sensible (comme ici, dans les graves), le niveau en dB SPL devra être plus élevé que le niveau en phones, et vice-versa.
Normes (la référence réglementaire)
Les calculs de perception auditive sont standardisés pour garantir la reproductibilité des résultats. Cet exercice s'appuie sur les données et les principes de la norme internationale ISO 226:2003, qui définit les courbes d'égale sonie pour un auditeur moyen.
Formule(s) (l'outil mathématique)
Formule générale
Hypothèses (le cadre du calcul)
Nos calculs reposent sur les hypothèses suivantes :
- L'auditeur est considéré comme "otologiquement normal", tel que défini par la norme ISO.
- Le son est un son pur (une seule fréquence) en champ libre (sans réverbération).
- Les valeurs d'ajustement \(A(f)\) fournies sont des approximations valides pour un niveau de 40 phones.
Donnée(s) (les chiffres d'entrée)
Les données d'entrée pour cette question sont le niveau de sonie cible et l'ajustement de sensibilité pour la fréquence de 100 Hz.
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Niveau de sonie cible | \(L_N\) | 40 | \(\text{phones}\) |
| Ajustement de sensibilité à 100 Hz | \(A(100)\) | +11.1 | \(\text{dB}\) |
Astuces (Pour aller plus vite)
Pour les fréquences inférieures à 1000 Hz, le facteur d'ajustement \(A(f)\) sera presque toujours positif pour les niveaux de sonie courants. Attendez-vous donc à trouver un résultat en dB SPL supérieur au niveau en phones.
Schéma (Avant les calculs)
Imaginons deux ondes sonores. Pour être perçues comme "égales", l'onde de 100 Hz doit avoir une amplitude (pression) physiquement plus grande que celle de 1000 Hz.
Amplitude pour une sonie égale de 40 Phones
Calcul(s) (l'application numérique)
Application de la formule
Calcul détaillé
Schéma (Après les calculs)
Nous pouvons maintenant placer notre premier point calculé sur le graphique, par rapport au point de référence de 1000 Hz.
Points sur la courbe 40 Phones
Réflexions (l'interprétation du résultat)
Le résultat de 51.1 dB SPL est significativement plus élevé que 40 dB. Cela quantifie notre intuition : pour qu'un son grave à 100 Hz nous paraisse aussi fort qu'un son médium de 40 dB, il doit être physiquement 11.1 dB plus intense. C'est la preuve que notre oreille est bien moins sensible dans les basses fréquences.
Points de vigilance (les erreurs à éviter)
L'erreur la plus commune est de confondre les échelles et de penser que 40 phones équivaut à 40 dB pour toutes les fréquences. Cette équivalence n'est vraie uniquement qu'à 1000 Hz. Pour toute autre fréquence, une conversion est nécessaire.
Points à retenir (permettre a l'apprenant de maitriser la question)
Pour maîtriser cette étape, retenez :
- La sonie (phones) est une perception, le niveau de pression (dB SPL) est une mesure physique.
- Dans les graves, la sensibilité de l'oreille diminue, donc \(L_p > L_N\).
- La formule de base est une simple addition : \(L_p = L_N + A(f)\).
Le saviez-vous ? (la culture de l'ingénieur)
Les sons de très basse fréquence (infrasons, < 20 Hz), bien qu'inaudibles, peuvent être ressentis par le corps et provoquer des sensations d'inconfort ou de malaise. Certains phénomènes naturels (vents, vagues) et industriels (ventilations) en génèrent en permanence.
FAQ (pour lever les doutes)
Résultat Final (la conclusion chiffrée)
A vous de jouer (pour verifier la comprehension de l'etudiant parrapport a la question)
Maintenant, à vous ! Calculez le niveau de pression requis à 63 Hz, sachant que son facteur d'ajustement A(63) est de +16.5 dB.
Question 2 : Calcul du Lp à 250 Hz
Principe (le concept physique)
Nous répétons le processus pour une fréquence de 250 Hz. Cette fréquence est encore dans les graves, mais plus proche des médiums. Nous nous attendons donc à ce que la sensibilité de l'oreille soit meilleure qu'à 100 Hz.
Mini-Cours (approfondissement théorique)
La transition entre les basses fréquences et les médiums est cruciale en acoustique. La fréquence de 250 Hz est souvent considérée comme la limite inférieure de la "chaleur" dans la musique. C'est là que se situe le corps des voix masculines et de nombreux instruments. Une bonne perception dans cette zone est essentielle à l'équilibre sonore.
Remarque Pédagogique (le conseil du professeur)
Le facteur d'ajustement de +3.8 dB est bien plus petit que le précédent (+11.1 dB). Cela doit immédiatement vous alerter : le résultat final en dB SPL sera beaucoup plus proche de 40 dB, confirmant que l'oreille "entend mieux" à 250 Hz qu'à 100 Hz.
Normes (la référence réglementaire)
La démarche reste encadrée par la norme ISO 226:2003, qui fournit les données de référence pour toutes les fréquences normalisées, y compris 250 Hz.
Formule(s) (l'outil mathématique)
Formule générale
Hypothèses (le cadre du calcul)
Les hypothèses sont les mêmes que pour la question 1 : auditeur normal, son pur en champ libre, et validité des coefficients d'ajustement.
Donnée(s) (les chiffres d'entrée)
Nous utilisons la nouvelle valeur d'ajustement fournie pour 250 Hz.
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Niveau de sonie cible | \(L_N\) | 40 | \(\text{phones}\) |
| Ajustement de sensibilité à 250 Hz | \(A(250)\) | +3.8 | \(\text{dB}\) |
Astuces (Pour aller plus vite)
Lorsque vous comparez deux fréquences, le simple fait de comparer leurs facteurs d'ajustement vous donne la réponse qualitative. \(A(250) < A(100)\), donc l'oreille est plus sensible à 250 Hz qu'à 100 Hz.
Schéma (Avant les calculs)
Comparé à la situation de 100 Hz, nous nous attendons à ce que l'amplitude requise pour le son de 250 Hz soit plus faible pour atteindre la même sonie perçue.
Comparaison des amplitudes requises
Calcul(s) (l'application numérique)
Application de la formule
Calcul détaillé
Schéma (Après les calculs)
Nous ajoutons ce nouveau point au graphique. Il se place logiquement entre le point à 100 Hz et celui à 1000 Hz, montrant la descente de la courbe.
Points sur la courbe 40 Phones
Réflexions (l'interprétation du résultat)
Le résultat de 43.8 dB SPL confirme nos attentes. Il ne faut "que" 3.8 dB de plus que le niveau de référence pour percevoir ce son comme étant à 40 phones. La sensibilité de l'oreille s'est nettement améliorée entre 100 et 250 Hz.
Points de vigilance (les erreurs à éviter)
Ne soyez pas surpris par la variété des valeurs de \(A(f)\). La sensibilité de l'oreille n'évolue pas de manière linéaire ou logarithmique simple ; sa courbe est complexe et issue de l'expérimentation.
Points à retenir (permettre a l'apprenant de maitriser la question)
Le point clé de cette question est de constater l'évolution de la sensibilité. Retenez que plus le facteur d'ajustement \(A(f)\) se rapproche de zéro, plus la sensibilité de l'oreille se rapproche de celle à 1000 Hz.
Le saviez-vous ? (la culture de l'ingénieur)
Le "brouhaha" ou le "rumble" que l'on cherche à éliminer dans les enregistrements audio (par exemple, le bruit d'un climatiseur) se situe souvent dans cette zone de 100-250 Hz. Les ingénieurs du son utilisent des filtres "passe-haut" pour l'atténuer sans affecter la clarté des voix.
FAQ (pour lever les doutes)
Résultat Final (la conclusion chiffrée)
A vous de jouer (pour verifier la comprehension de l'etudiant parrapport a la question)
À votre tour ! Calculez le niveau de pression requis à 500 Hz, sachant que son facteur d'ajustement A(500) est de +0.8 dB.
Question 3 : Calcul du Lp à 1000 Hz
Principe (le concept physique)
Cette question est une pure vérification de la définition de l'échelle de sonie. Nous devons simplement confirmer mathématiquement que, pour la fréquence de référence, les échelles de pression physique (dB SPL) et de perception (phones) coïncident.
Mini-Cours (approfondissement théorique)
Toutes les échelles de mesure perceptives (comme les phones, mais aussi les échelles de luminosité, de goût, etc.) nécessitent un "point d'ancrage" ou une référence arbitraire pour être définies. En psychoacoustique, la communauté scientifique a choisi le son pur de 1000 Hz comme étalon universel. C'est un son médium, facilement reproductible, et situé dans une zone de bonne sensibilité pour la plupart des gens.
Remarque Pédagogique (le conseil du professeur)
Cette question peut sembler "trop simple", mais elle est fondamentale. Si vous ne trouvez pas 40 dB, c'est qu'il y a une erreur de compréhension du concept de base. C'est un excellent point de contrôle pour vous assurer que vous avez bien saisi la définition du phone.
Normes (la référence réglementaire)
La définition même du phone est inscrite dans la norme ISO 226:2003. La norme stipule que le niveau de sonie en phones est numériquement égal au niveau de pression en dB SPL pour un son de 1000 Hz.
Formule(s) (l'outil mathématique)
Formule générale
Hypothèses (le cadre du calcul)
Aucune hypothèse supplémentaire n'est nécessaire ; nous appliquons simplement une définition.
Donnée(s) (les chiffres d'entrée)
Par définition, l'ajustement de sensibilité à la fréquence de référence est nul.
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Niveau de sonie cible | \(L_N\) | 40 | \(\text{phones}\) |
| Ajustement de sensibilité à 1000 Hz | \(A(1000)\) | 0 | \(\text{dB}\) |
Astuces (Pour aller plus vite)
Pas besoin de calculatrice ! Pour 1000 Hz, la réponse en dB SPL est TOUJOURS égale à la question en phones. C'est la règle du jeu.
Schéma (Avant les calculs)
Le schéma conceptuel est celui de l'équivalence : l'amplitude de l'onde à 1000 Hz définit la référence pour toutes les autres.
Équivalence à la Fréquence de Référence
Calcul(s) (l'application numérique)
Application de la formule
Calcul détaillé
Schéma (Après les calculs)
Ce point est le pivot central de notre courbe. Toutes les autres valeurs s'organiseront autour de lui.
Le point d'ancrage de la courbe
Réflexions (l'interprétation du résultat)
Ce résultat n'est pas une découverte mais une confirmation. Il ancre notre courbe isosonique : nous savons maintenant avec certitude qu'elle doit passer par le point (1000 Hz, 40 dB). C'est le seul point commun à toutes les échelles de mesure du volume sonore.
Points de vigilance (les erreurs à éviter)
Attention à ne pas généraliser cette règle. L'équivalence \(L_p = L_N\) n'est valable qu'à 1000 Hz. Appliquer cette règle à 2000 Hz ou 500 Hz est une erreur fréquente.
Points à retenir (permettre a l'apprenant de maitriser la question)
La seule chose à maîtriser ici est la définition : 1 phone = 1 dB SPL à 1000 Hz. Cette phrase est le pilier de toute la psychoacoustique de la sonie.
Le saviez-vous ? (la culture de l'ingénieur)
Le son de référence à 1000 Hz est universellement utilisé pour calibrer les équipements audio, des sonomètres aux casques d'écoute, en passant par les systèmes de diffusion sonore. C'est le "La" 440 Hz du monde de l'acoustique technique.
FAQ (pour lever les doutes)
Résultat Final (la conclusion chiffrée)
A vous de jouer (pour verifier la comprehension de l'etudiant parrapport a la question)
Si un son à 1000 Hz a un niveau de pression de 60 dB SPL, quel est son niveau de sonie ?
Question 4 : Calcul du Lp à 4000 Hz
Principe (le concept physique)
Nous explorons maintenant une fréquence dans les haut-médiums (4000 Hz ou 4 kHz). C'est une zone où l'oreille humaine est connue pour être particulièrement sensible, nous nous attendons donc à un résultat en dB SPL inférieur à 40.
Mini-Cours (approfondissement théorique)
La sensibilité accrue de l'oreille autour de 3-4 kHz est due à un phénomène de résonance. Le conduit auditif externe, par sa forme et sa longueur (environ 2.5 cm), agit comme un tuyau résonant qui amplifie naturellement les fréquences dans cette plage. Cette amplification "gratuite" signifie que le tympan reçoit une pression acoustique plus élevée que celle présente dans l'air ambiant, d'où la perception d'un son plus fort.
Remarque Pédagogique (le conseil du professeur)
C'est la première fois que vous rencontrez un facteur d'ajustement négatif. Cela doit immédiatement vous indiquer que l'oreille est plus sensible à cette fréquence qu'à 1000 Hz. Pour obtenir la même sonie, le son doit être physiquement moins intense.
Normes (la référence réglementaire)
La norme ISO 226:2003 modélise précisément ce pic de sensibilité autour de 4 kHz, qui est une caractéristique universelle de l'audition humaine.
Formule(s) (l'outil mathématique)
Formule générale
Hypothèses (le cadre du calcul)
Les hypothèses sont les mêmes que pour les questions précédentes : auditeur normal, son pur en champ libre, et validité des coefficients d'ajustement.
Donnée(s) (les chiffres d'entrée)
Nous utilisons la valeur d'ajustement négative pour 4000 Hz.
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Niveau de sonie cible | \(L_N\) | 40 | \(\text{phones}\) |
| Ajustement de sensibilité à 4000 Hz | \(A(4000)\) | -8.2 | \(\text{dB}\) |
Astuces (Pour aller plus vite)
Un \(A(f)\) négatif est le signe d'une zone de haute sensibilité. Attendez-vous à ce que le point le plus bas de la courbe ("le creux de la baignoire") se trouve près de ces fréquences.
Schéma (Avant les calculs)
Pour cette fréquence, l'amplitude de l'onde requise sera encore plus faible que celle de notre référence à 1000 Hz pour atteindre la même perception d'intensité.
Amplitude requise à 4 kHz (Haute Sensibilité)
Calcul(s) (l'application numérique)
Application de la formule
Calcul détaillé
Schéma (Après les calculs)
Ce point se situe en dessous de la ligne des 40 dB sur notre graphique, formant le creux de la courbe.
Le creux de la courbe à 4 kHz
Réflexions (l'interprétation du résultat)
Un niveau de pression de seulement 31.8 dB est nécessaire pour paraître aussi fort qu'un son de 40 dB à 1000 Hz. Cela confirme quantitativement l'hypersensibilité de notre audition dans cette plage de fréquences, un avantage évolutif pour la communication et la détection de dangers.
Points de vigilance (les erreurs à éviter)
N'oubliez pas le signe "moins" ! Une simple erreur d'inattention transformerait une zone de haute sensibilité en zone de faible sensibilité et inverserait complètement la logique du résultat.
Points à retenir (permettre a l'apprenant de maitriser la question)
Ce qu'il faut maîtriser :
- Un facteur \(A(f)\) négatif signifie une sensibilité supérieure à celle de la référence (1000 Hz).
- La zone 2-5 kHz est la plus sensible de l'audition humaine.
- Cette sensibilité est due à la résonance du conduit auditif.
Le saviez-vous ? (la culture de l'ingénieur)
Cette hypersensibilité autour de 3-4 kHz est un héritage de l'évolution. Elle nous a permis de mieux distinguer les composantes essentielles de la voix humaine (les consonnes "s", "f", "t") et les sons d'alerte dans la nature, comme le craquement d'une branche ou le cri d'un bébé.
FAQ (pour lever les doutes)
Résultat Final (la conclusion chiffrée)
A vous de jouer (pour verifier la comprehension de l'etudiant parrapport a la question)
Pour finir, calculez le niveau de pression requis à 2000 Hz, sachant que son facteur d'ajustement A(2000) est de -2.8 dB.
Question 5 : Description de la courbe
Principe
L'objectif est de synthétiser les résultats précédents en traçant les points et en interprétant la forme globale de la courbe pour comprendre le comportement de l'audition.
Schéma (Après les calculs)
En reportant les points calculés (100 Hz, 51.1 dB), (250 Hz, 43.8 dB), (1000 Hz, 40 dB) et (4000 Hz, 31.8 dB) sur un graphique, on obtient l'esquisse de la courbe isosonique de 40 phones.
Esquisse de la courbe 40 Phones
Réflexions
La courbe a une forme de "U" ou de "baignoire". Elle est très élevée dans les basses fréquences, descend pour atteindre un point bas dans les médiums-aigus (vers 4 kHz), puis remonte légèrement dans les très hautes fréquences (non calculé ici).
Cette forme illustre parfaitement la sensibilité de l'oreille :
Points à retenir
La forme en "U" des courbes isosoniques est une caractéristique fondamentale de l'audition humaine. C'est pourquoi les égaliseurs audio ont souvent des contrôles pour les "basses" et les "aigus", car ce sont les zones où notre perception du volume change le plus.
Outil Interactif : Simulateur de Courbes Isosoniques
Utilisez les curseurs pour explorer comment le niveau de pression acoustique (dB SPL) requis change en fonction de la fréquence et du niveau de sonie (phones) souhaité. Le graphique ci-dessous tracera la courbe isosonique complète pour le niveau de sonie sélectionné.
Paramètres d'Entrée
Graphique Dynamique
Le graphique ci-dessous est mis à jour en temps réel pour montrer la courbe d'égale sonie correspondant au niveau de phones que vous avez sélectionné.
Quiz Final : Testez vos connaissances
1. Quelle est l'unité du niveau de sonie, qui représente l'intensité perçue d'un son ?
2. Par définition, à quelle fréquence le niveau en phones est-il égal au niveau en dB SPL ?
3. Dans quelle plage de fréquences l'oreille humaine est-elle généralement la plus sensible (nécessitant le moins de dB SPL pour être entendue) ?
4. Un son de 80 Hz à 65 dB SPL et un son de 1000 Hz à 50 dB SPL sont perçus comme ayant la même sonie. Quel est leur niveau de sonie commun ?
5. Que signifie le fait que les courbes isosoniques se "resserrent" (deviennent plus plates) à des niveaux de sonie élevés ?
Glossaire
- Courbe Isosonique
- Une courbe représentant l'ensemble des sons purs (fréquence, niveau de pression) qui sont perçus par un auditeur comme ayant le même niveau de sonie.
- Décibel (dB SPL)
- Unité de mesure du niveau de pression acoustique (Sound Pressure Level). C'est une mesure physique et objective de l'intensité d'un son, basée sur une échelle logarithmique.
- Fréquence
- Le nombre d'oscillations d'une onde sonore par seconde, mesuré en Hertz (Hz). La fréquence détermine la hauteur perçue d'un son (grave ou aigu).
- Phone
- Unité du niveau de sonie. Elle est subjective et définie par comparaison perceptive avec un son de référence de 1000 Hz.
- Psychoacoustique
- La branche de la science qui étudie la relation entre les stimuli sonores physiques et la sensation auditive psychologique qu'ils produisent.
- Sonie
- Attribut subjectif d'un son qui permet à un auditeur de le classer sur une échelle allant de "faible" à "fort". C'est l'équivalent perceptif de l'amplitude ou de l'intensité physique.
D’autres exercices de Psychoacoustique:
Étude de l’Effet de Précédence (ou Effet Haas)
Exercice : Effet de Précédence (Effet Haas) Étude de l’Effet de Précédence (ou Effet Haas) Contexte : La psychoacoustiqueLa branche de la psychophysique qui étudie la relation entre les stimuli sonores physiques et les sensations auditives qu'ils produisent. et la...
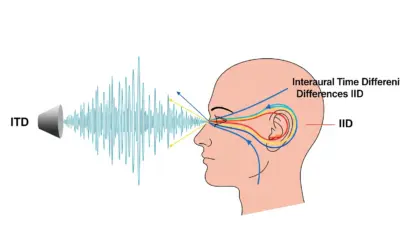
Rôle des Indices de Temps (ITD) et d’Intensité (IID)
Exercice sur la Localisation Sonore : ITD et IID Localisation Sonore : Rôle des Indices de Temps (ITD) et d’Intensité (IID) Contexte : La PsychoacoustiqueBranche de la science qui étudie la perception subjective des sons par l'être humain.. La capacité à localiser une...
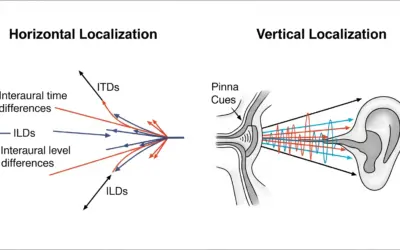
Distinction entre la Localisation Sonore
Exercice : Distinction entre la Localisation Sonore Distinction entre la Localisation Sonore Contexte : La scène auditive 3D. Notre cerveau est capable de construire une représentation tridimensionnelle de notre environnement sonore à partir des signaux captés par nos...
Phénomène de la Fondamentale Manquante
Phénomène de la Fondamentale Manquante Phénomène de la Fondamentale Manquante Contexte : La perception de la hauteur tonaleAttribut perceptif d'un son qui permet de le classer sur une échelle allant du grave à l'aigu.. La perception auditive humaine est un processus...
Hauteur Tonale (Pitch) Perçue d’un Son
Calcul de la Hauteur Tonale (Pitch) Perçue d’un Son Calcul de la Hauteur Tonale (Pitch) Perçue d’un Son Contexte : La PsychoacoustiqueBranche de la science qui étudie la perception subjective des sons par l'être humain, en liant les propriétés physiques d'un son à la...
Analyse de l’Effet de Masquage Temporel
Analyse de l’Effet de Masquage Temporel en Psychoacoustique Analyse de l’Effet de Masquage Temporel Contexte : La PsychoacoustiqueLa psychoacoustique est la branche de la psychophysique qui étudie la perception subjective des sons par l'oreille humaine.. Cet exercice...

0 commentaires